Back to History files. Back to home page.

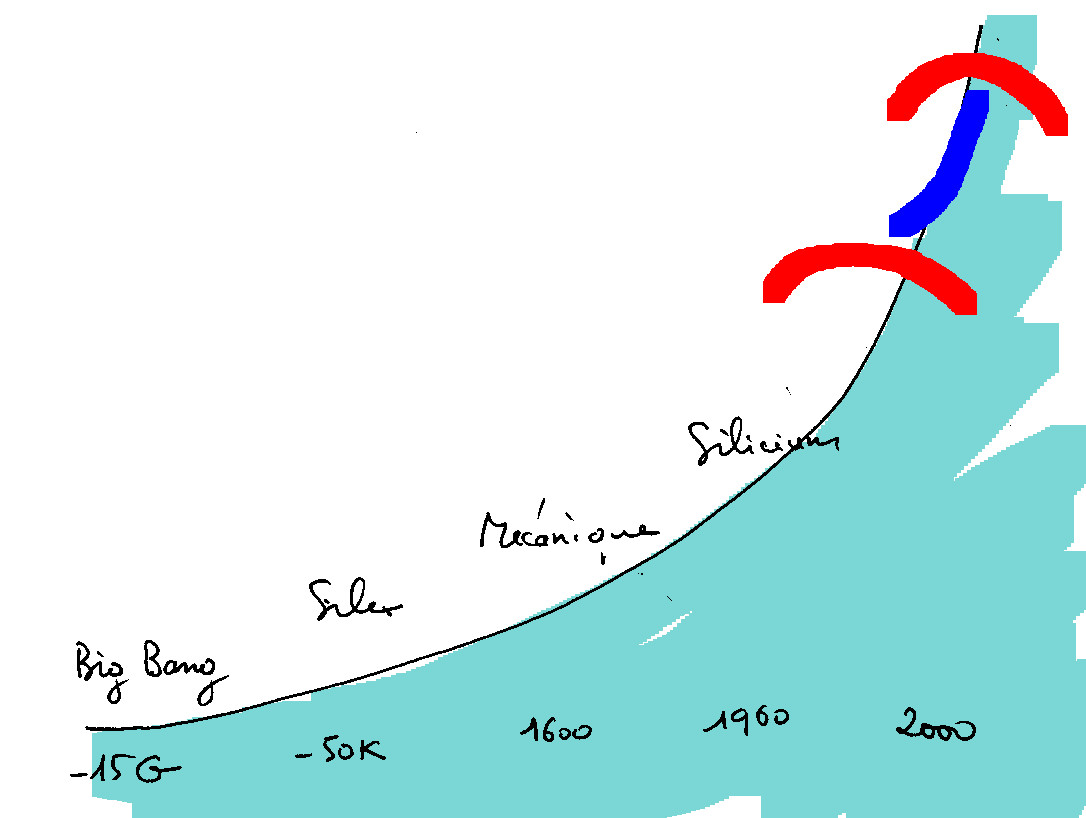
Une loi de croissance historique digitale (LHD)

Club de L'hypermonde. Groupe Histoire quantitative de l'informatique. 1999 . Petites Révisions en 2010, 2013, 2017 Pierre Berger

Ce texte tient compte d'idées et suggestions apportées par les autres membres du groupe, notamment Jean-Claude Debeir, Victor Sandoval et Michel Volle, puis de participants aux réunions de travail de Pierre Mounier-Kuhn, et enfin d'observations d'Alain Le Boucher.

Au 2 septembre 2013, il y a des raisons de douter de la validité actuelle de la loi de Moore. 23

Au 23 avril 2020, la loi de Moore, effectivement, ne s'applique plus. En partie pour des raisons de dissipation thermique. On cherche différents moyens de repartir : très gros investissements sur les calculateurs quantiques, et quelques expériences sur les circuits biologiques (DNA computing).

1. La loi de Moore : 40 ans de validité

>La loi de Moore d’origine est purement technique. Sa formulation par Gordon Moore, alors employé par Fairchild et, par la suite, co-fondateur d’Intel, remonte à 1964 [Ceruzzi 1998]. Il observa, simplement en reportant les chiffres sur du papier quadrillé semi-logarithmique, que, depuis l’invention des circuits intégrés en 1958, le nombre de circuits que l’on pouvait placer sur un seul circuit intégré doublait tous les deux ans. Il en déduisit que, vers le milieu des années 70, on pourrait acheter des puces de puissance équivalente à un mainframe des années 50. La loi s’est toujours vérifiée depuis, soit sur plus de 40 ans, bien que le rythme se soit accentué ces dernières années, et qu’on fait en général état d’un doublement tous les 18 mois plutôt que deux ans.

En pratique, la communauté informatique l'a appliqué à de nombreux aspects fonctionnels et économiques du monde digital et elle peut s’exprimer familièrement : « On en a deux fois plus tous les ans pour le même prix tous les deux ans ».

Le « en » peut s’exprimer en  puissance de processeur, des capacité de disque, bande passante, résolution en pixels ou disponibilité d’impression. Le prix se mesure en unités monétaires (dollars, euros) ou matérielles (quantités de silicium ou autres matériaux magnétiques, pris tant au niveau de la puce elle-même que de l’ensemble de son conditionnement).

2. Une loi importante et fascinante

Outre son importance économique cruciale, et les enjeux qui s’attachent à la poursuite de sa validité dans les décennies à venir, cette loi a un caractère très original, du point de vue épistémologique, qui justifierait à lui seul d’importants efforts pour la valider, la préciser ou la falsifier (au sens de Popper). C’est pourquoi elle s’inscrit en bonne place dans les objectifs du groupe « Histoire quantitative de l’informatique ". 

Elle fascine par son caractère à la fois naturel et artificiel.

D'une part elle a un caractère naturel. On peut en vérifier objectivement la réalisation (mais aussi en évaluer la précision, et le périmètre de validité) sur le marché des produits informatiques et plus généralement des nouvelles technologies de la communication. Elle est  aussi observable que la récurrence des éclipses ou le rythme d’évolution des espèces en paléontologie. La grande régularité de sa réalisation depuis sa formulation par renforce cette impression.

D’autre part, elle artificielle, puisque technologie et prix sont l’œuvre de l’intelligence et de la volonté des humains qui les produisent, du désir de leurs consommateurs et de la stratégie des vendeurs et acheteurs qui opèrent sur les marchés. Et on peut d’autant plus suspecter l’artifice que Gordon Moore est un des acteurs importants de ces marchés. Certains parlent de « prophétie auto-réalisatrice », visant des objectifs commerciaux et faisant jouer une « loi de Parkinson » des logiciels (que Myrhwold, un adjoint de Bill Gates, constate de son côté en disant que le logiciel est un gaz parfait qui remplit tout l’espace qu’on lui octroie).

Son succès résulte particulièrement d'une coopération permanente entre les acteurs mondiaux du domaine. Ils rédigent en particulier, de temps en temps, l'ITRS (International technology roadmap for semiconductors), que l'on peut télécharger à partir du site ITRS.

Il est vrai que cela est vrai pour la plupart des lois économiques, par exemple la loi de Philips (?) sur les relations entre chômag et inflaction, qui s'est toujours vérifiée sauf à la fin des années 70 avc la stagflation.

Ne serait-ce que pour ce statut surprenant, il semble intéressant de chercher à préciser les limites de validité de cette loi, d’en trouver les causes ou d’en modéliser la réalisation, et de voir si elle peut s’étendre à d’autres domaines, ou si elle n’est pas le cas particulier d’une loi plus générale.

3. Tentative de généralisation : une loi historique digitale

Mais il est tentant aussi de la considérer comme un cas particulier d'une loi plus générale.  L’idée m’en a été suggérée par la courbe établie par Leroi-Gourhan [Leroi-Gourhan 65] sur l’évolution des silex au cours des ères préhistoriques, où le "en" (du "on en a deux fois plus")  s’exprime en mètres de tranchant et le prix en kilos de silex brut. Ici encore, la courbe est exponentielle, mais sur environ des dizaines de milliers d’années et non sur trente ans.

Cet intérêt vient encore d'être relancé par la parution du rapport Chaline/Nottale/Grou [Chaline 99], qui fixerait la chronologie de l'évolution des êtres vivants par la formule :

T_n = T_c  + ( T_o   +  T_c ) g ^-n

T_n  : grande date de mutation<
T_o : origine de la lignée
T_c  : temps critique où elle perd son potentiel évolutif
g  : rapport de longueur d'une branche à ses sous-branches.

Cette formule et cette théorie sont d'ailleurs largement contestés. Les objections ne nous semblent pas suffisantes pour nous éloigner de notre objectif.

Pour notre part, en partant de la loi de Moore, nous  proposons la formule générale suivante, que nous appellerons LHD (Loi historique digitale) :

« A un moment donné de l’histoire, le rendement des technologies dominantes s’accroît de manière sensiblement exponentielle, l’exposant étant caractéristique de la période en cours ».

Notes :

A un moment donné, cela peut jouer de manière tout à fait différente selon les technologie. En particulier, les technologiques, sauf le hors sol, pasente par des stagnations, définies par les lois de cette surface de transformation énergétique qu'est la parcelle. Et puis il y a des ruptures : le collier d'épaule, l'abandon de la jachère avec l'assollement trienneal et la fumure..

Tant qu'on n'a que le cheval, au bout de 30 kilomètres, il mange sa charge. D'où l'importance des fleuves, de la mer, pour l'élargissemetnd es marchés.

Il y a un saut majeur au XIIIe, un autre au XVIIIe.

Et, tant qu'à s'avancer dans les conjectures, nous prendrons le risque, ad experimentum, d’étendre le concept de « technologie » à tout mode général de réalisation de fonctions par des organes. Donc de considérer la physico-chimie neuronale comme une technologie parmi d’autres. L'accélération de l'histoire, par exemple, devient un cas particulier de la LHD.

On peut même aller encore plus loin, et pousser jusqu'à "tout type d'organisation", ce qui permet d'y inclure la physique nucléaire et la cosmologie générale, et donc d'étendre la loi jusqu'au big bang originel.. Ajoutons-y les organisations "sociales" (entreprises, collectivités ou communautés politiques).

On trouve un tel élargissement chez Kurzweil, avec ses Canonical Milestones. Mais il y a certainement bien d'autres auteurs sur cette façon de voir le monde.

4. Explicitons les paramètres

Bien entendu, plus la proposition sera générale, plus il faudra étendre le sens des mots, en particulier celui de "rendement". Précisons sur les paramètres de la formule, avant d’entrer dans le détail des différentes zones où nous envisageons de l’étendre. 

Le rendement est le rapport entre la valeur fonctionnelle d’un système (plus exactement sous-système, on verra plus loin pourquoi) et son coût. Il n’est pas indispensable, pour que l’on puisse étudier la loi et sa validité sur le terrain, que la valeur fonctionnelle et le coût se mesurent dans les mêmes unités [Dhombres 98]. Cependant une bonne généralisation de la loi doit permettre de comparer et de combiner différentes technologies (voir plus loin). Il faut donc chercher une mesure aussi universelle que possible.

Nous proposons d’utiliser au numérateur comme au dénominateur la complexité descriptionnelle ou générative, dite complexité de Kolmogorov, c’est à dire la longueur du plus petit programme qui permet à une machine de référence de générer l’objet décrit . On pourrait aussi se baser sur la « profondeur logique » de Bennett (nombre de cycles nécessaires à une machine de référence pour générer l’objet). Ou une combinaison des deux. (Sur ces concepts, voir [Delahaye 99]). Ces définitions de la complexité ou du coût d’obtention d’un objet ne portent directement que sur les chaînes binaires. L’élargissement et la LDH dépend donc de la qualité des méthodes qui permettent de ramener les différents objets à de telles chaînes, visant à les décrire ou à engendrer le processus de leur génération.

Au numérateur, nous parlerons de complexité fonctionnelle. Il s’agit de la variété et du degré de perfectionnement de la fonction que remplit le système, ou des différentes fonctions qui contribuent à sa valeur. On pourrait se rapprocher ici des concepts de l’analyse de la valeur, bien que cette méthode soit rarement quantifiée à ce point.

Au dénominateur, nous parlerons de complexité organique, c’est à dire le nombre des organes ou composants, le degré de sophistication de leur assemblage et leur complexité élémentaire.

Voyons comment ces concepts s’étendent à des catégories de plus en plus large de « systèmes ». Sans dissimuler que les difficultés à vaincre ne seront pas minces pour que les formulations soient non seulement correctes, mais significatives.

5. Application au logiciel

L’approche est relativement naturelle pour les données et les logiciels, chaînes binaires par construction. En première approche, leur complexité organique se ramène à leur masse binaire : méga ou giga-octets, nombre d’enregistrements, nombre de lignes de code.

Cependant, dans leur état opérationnel, leur écriture laisse place à une énorme redondance, pour des raisons d’efficacité. On peut se rapprocher de la complexité théorique avec des programmes classiques de compression. Mais il serait plus intéressant de le faire avec des générateurs de programmes inspirés du génie logiciel. 

Quant à leur complexité fonctionnelle, la méthode des points de fonction permet une quantification considérée comme raisonnable selon l’expérience de nombreuses entreprises… qui n’y recourent cependant qu’avec modération car le calcul même de ces points présente un coût non négligeable. Il faudrait explorer ici les classiques de l’économie du logiciel à commencer par [Boehm 82]. Il est bien connu que le coût de la ligne de code tend à ne pas baisser, et que le logiciel ne se conforme pas du tout à la LHD.

Cela peut s’expliquer en partie par le fait qu’on demande au logiciel d’intégrer une partie de la complexité, y compris celle du matériel, par le biais du micro-codage des lignes d’instruction. Les exigences en fiabilité croissent aussi fortement d’année en année. Tout utilisateur d’un logiciel du commerce peste régulièrement contre les bogues qui perturbent son travail. Mais l’observateur peut tout aussi biens s’émerveiller du simple fait que des logiciels aussi compliqués parviennent tout simplement à fonctionner.

Mais surtout, cette non augmentation de la productivité tient au fait que l’on ne tient pas compte du nombre de logiciels livrés. Dans une entreprise, même si un logiciel est diffusé sur des milliers de postes, ou qu’un logiciel central est exploité à partir de milliers d’agences locales, on mesure toujours les coûts à la ligne de code d’origine. Autrement dit on ne considère que des logiciels prototypes, sans tenir compte dans le calcul de leur industrialisation et du coût pratiquement nul de leur multiplication par pressage de CD-Roms ou par téléchargement.

Notes pour des mesures sur le logiciel

Il est très difficile de mesurer le logiciel. Proposons quelques pistes :

- Sur le code lui-même : prix, encombrement, temps de calcul consommé
- Sur le fonctionnnement : points de fonction, complexité descriptionnelle
- Contribution à la valeur de l'entreprise
- Fiabilité, durée de vie

6. Application aux matériels numériques

La matériels digitaux (processeurs, periphériques, lignes de télécommunications) suivent la loi de Moore avec une régularité remarquable. Voir par exemple le travail de François Anceau in [Bloch 99] ou les analyses d’indices de Michel Volle [Volle 00]

Un peu plus éloignés des chaînes binaires proprement dites, les matériels informatique peuvent cependant assez bien se prêter à la métrique de Kolmogorov.

Le « nombre de circuits » employé par Gordon Moore peut fournir la base à une mesure en complétant le comptage par une mesure du graphe des relations.

Plus finement, comme les circuits électroniques sont conçus et réalisés à l’aide de logiciels de CAO et de FAO, la longueur même de ces programmes et des fichiers de données apporte une excellente base.

Quant aux fonctions, leur description est fortement encadrée par les lois même du marché qui conduisent à la marginalité sinon à l’extinction toute les structures qui s’éloignent des standards : la machine de Von Neumann, ses mémoires, ses lignes de communication.

Cela dit, pour une bonne agrégation des fonctions au sein d’un système donné, il faudrait disposer d’une unité permettant d’additionner les performances des circuits de calcul, des mémoires et des liaisons à distance.

Une idée de mesure générale en numérique : les "ops"

Nous proposons d’étudier par exemple une unité baptisée « ops », cohérente en dimension avec bits²/sec.

. Pour les mémoires, le nombre d’ops est égal à la capacité multiplié par le taux de transfert. Par exemple un CD-Rom de 650 méga-octets, soit 6 milliards de bits totalement lu en dix minutes, soit 600 secondes, taux de transfert 10 mégabits/sec, puissance globale 60 Gops.

. Pour les processeurs, on met au numérateur le carré de la longueur du mot de référence (32 bits sur les PC actuellement), rapporté au nombre d’instructions par seconde. Cette formule est un peu artificielle, mais rend bien compte de l’importance de cette longueur de mot aussi bien sur la variété des instructions que sur la longueur des opérandes.
Exemple. Un processeur 32 bits à 400 MHz. 32.32 = 1024, 1024. Puissance globale : 400 Gops

. Pour les lignes de communication, on multiplie la bande passante, comptée en bits par seconde, par la longueur de la ligne mesurée en bits (étant donné que la vitesse est constante, sensiblement égale à celle de la lumière), à une bande passante donnée correspond une certaine distance sur la ligne entre bits successifs. Cela fait doublement intervenir la bande passante, puisque le nombre de bits par unité de longueur est d’autant plus grand que la bande passante est élevée.
Exemple : Une ligne de téléphone de 100 kilomètres utilisée à 54 Kilobits/seconde. A cette vitesse, il y a environ 60 kilobits répartis sur 300 000 km. Il y un bit tous les cinq kilomètres, soit 20 pour 100 kilomètres. Puissance globale : 60000 < 20 : 12 mégops.

On pourrait ainsi additionner la puissance des différents composants d'un système, même s'ils sont de nature différentes. Mais des calculs raisonnables, pour un système donné, devront faire intervenir des facteurs de combinaison limitatifs.

Selon le point de vue, on peut prendre les mesures en ops comme une complexité organique (les matériels étant considérés comme des organes pour le logiciel et les données) ou comme une complexité fonctionnelle (décrivant la fonction de systèmes dont il restera à mesurer la complexité organique, le coût d’obtention, par analyse des programmes de CAO, etc.). Il y a tout un travail à faire ici sur les coûts/avantages de l'intégration. Voir par exemple les travaux de Titli sur la commande hiérarchisée.

Hellinger propose une formule métrique :
Taux de croissance =  Delta x  multiplé par Delta x   /x  soit (Deta x)²/x

7. Extension aux autres produits fabriqués (artefacts)

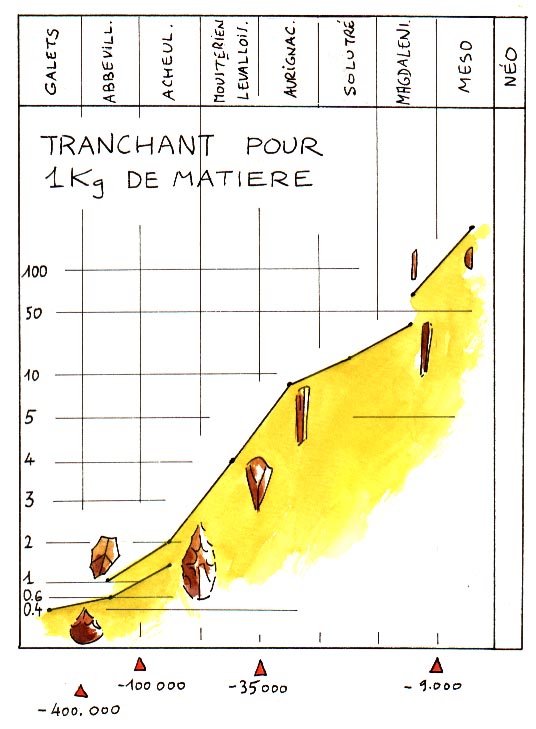
On trouve chez Leroi-Gourhan une loi d'évolution des silex taillés selon la longueur de tranchant rapportée au poids.

Simondon s'intéresse aux structures, sans critères quantitatifs.

Plus on s’éloigne des produits informatiques, plus les mesures vont devenir difficiles. Ce qui se fait à la machine est plus facile à mesurer qu’un produit artisanal…

La complexité des pièces électroniques, mécaniques ou optiques se laisse bien appréhender par la longueur des programmes qu'il faut fournir aux machines-outils qui les usinent ou les réalisent. Moyennant un facteur multiplicatif approprié pou tenir compte de la complexité même de ces machines de production par rapport à la machine de référence.

Les quantités de matière utilisée appellent une formule donnant la « densité de complexité » d’un matériau donné. Cela n’a rien d’aberrant a priori, d’autant que le progrès technologique passe notamment par des matériaux de plus en plus élaborés, soit par leur complexité à proprement parler (fibre de carbone) soit par leur pureté (qui est une forme particulière de complexité, de même que  10,0000000  est plus précis que 10).

Les quantités d'énergie consommées font problème car, idéalement, il s'agit d'énergies pures, non structurées.

Cela nous conduit à un problème général et clé : ce qui est pur est difficile et coûteux à obtenir. Et pourtant, sa complexité descriptionnelle tend vers zéro, et ne dépend nullement des quantités consommées. Ce point est peut-être une difficulté facile à résoudre. Ou au contraire, c'est une des failles qui montrent la nécessité de faire intervenir la relativité digitale. En effet, au déjà de certaines limites, il coûte très cher d'accroître les dimensions d'un objet de structure pure, et on finit par buter sur des limites. C'est le cas des cristaux, mais la règle est générale.

Un problème analogue se pose pour la précision, qui peut être très chère à obtenir. Mais ici, a priori, la complexité descriptionnelle la prend en compte, plus facilement que la pureté.

Les coûts sont à la fois particulièrement intéressants et particulièrement difficiles à prendre en compte. Ils peuvent intervenir au numérateur et/ou au dénominateur. S’ils interviennent dans les deux, le ratio est un rendement au sens comptable, ou une marge. S’ils interviennent au numérateur, il s’agit d’une valeur d’usage. Au dénominateur, d’un coût d’acquisition.  N’espérons par trop traiter en quelques lignes la théorie de la valeur, qui a fait couler beaucoup d’encre ;

Par ailleurs, le rendement étudié par la LHD s’applique aussi bien à des puissances, comprenant des fréquences, qu’à des données statiques (capacités). Cela n’est pas contradictoire (une machine ne cesse pas de fonctionner à un gigahertz même si on examine ses propriétés à un instant défini à un dix-milliardième de seconde. De même qu’une économie peut être dans un cycle de croissance même si le PIB a baissé d’un mois sur l’autre. Il faudra cependant sans doute y faire attention.

Pour les entreprises, on pourrait avoir :
- une métrique organique ( effectifs, achats, capital immobilisé);
- une métrique fonctionnelle : chiffre d'affaires, bénéfice, produits livrés, dividendes

8. Les objets naturels, et tout particulièrement les objets biologiques

Les objets naturels se prêtent à ces mesures dans la mesure même où nous savons les réduire, ou acceptons de les réduire, à une description digitale.

Un premier obstacle vient de la puissance du continu. Mais, note Delahaye, il ne faut pas s’exagérer cette difficulté. Car les modèles actuels des physiciens sont plus discrets que continus. Citons- le

« Le physicien n’exisge pas qu’on prenne le continu au sérieux. Donnons-en deux preuves. D’abord il est bien clair pour un physicien qui écrit les équations de la chaleur qu’il approxime la matière discrète (composée d’atomes) par de la matière continue, e que c’est parce que l’approximation du discret par le continu lui donne une équation simple qu’il procède ainsi… Une autre preuve… est fournie par l’absence totale de l’utilisation de la non-dénombrabilité en physique : la question « y a-t-il une infinité dénombrable de points dans un centimètre cube d’espace ? » n’a de sens pour aucun physicien. » [Delahaye 99]

Accessoirement, on peut se poser la question langagière : a-t-on le droit d’employer les mêmes mots (mémoire, cerveau, communication, neuronal…) pour le vivant et pour les machines ? Il y a là quelque chose de sacrilège. Mais y renoncer serait jeter à l'égout l’essentiel de la cybernétique, une grande partie de la systémique (l’une et l’autre s’étant à la base développées sur l’utilité et la fécondité de discourir dans les mêmes termes sur l’homme et la machine) et sinon de l’informatique elle-même, du moins du discours à son sujet. Le tout au niveau mondial et non pas seulement en France. Voir ici notament [Bloch].

A fortiori, l'extension de la loi jusqu’aux origines de l’univers conduit à un évident abus de langage à employer les termes d’organe et de fonction pour les molécules et leurs atomes, ou pour les atomes et les ensembles de particules (noyau, couches d’électrons) qui les constitue. Mais ici encore nous prendrons le risque, sous réserve d’inventaire. D’ailleurs, renoncer à employer les mêmes mots pour parles des hommes et des machines, ce serait jeter aux orties toute la systémique et derrière elle toute la cybernétique.

Le choix de la complexité descriptionnelle permet de tourner ces difficultés, en se donnant des moyens "objectifs" de mesure des paramètres en cause, quelque soit leur substrat organique (biologique ou minéral, naturel ou artificiel). Mais cela conduit à une question épistémologique plus profonde. Le choix de la complexité descriptionnelle comme système généralisé de mesure donne un rôle central à la machine. Il faudra donc ne jamais oublier dans les conclusions que l’on pourrait en tirer du point de vue économique et a fortiori du point de vue éthique et politique. (Nous y reviendrons). Il y a sans doute là un risque de circularité : en voyant les choses, et les hommes eux-mêmes, du point de vue de la machine, ne courons nous pas le risque d’une tautologie ? Du point de vue de la machine, elle seule compte, et notre transcendance lui échappe.

Nota : en quelque sorte, cela "tient par le haut" (serait une formule de Teilhard)

Et, en pratique, peut-on parler de quelque chose autrement que comme d’une machine ? En pratique, seul le récit ou le discours didactique peuvent y échapper. Et encore sous leur forme orale, car à partir du moment où ils sont écrits, ils se trouvent externalisés et donc eux-mêmes transformés sinon en machines du moins en outil.

En fait l’externalisation fondamentale naît avec les Grecs, Aristote en particulier, et le syllogisme. C’est le moment où, pour parler de quoique ce soit et en particulier des hommes (et de l’homme par excellence à l’époque, Socrate), on admet de faire confiance à autre chose qu’à l’intuition personnelle ou collective, ou à l’autorité d’une autre personne (père, chef, prêtre, sibylle) pour s’en remettre à un mécanisme externe, le syllogisme. Avec la conséquence radicale, bien vue par Aristote lui-même, que l’on crée une schize radicale entre le sens et la structure. A la fin du Moyen-Age, Bacon s’en réjouit et veut que la logique guide la pensée sur des voies sûrs « comme par des machines ».

Le fossé, bien sûr n'a fait que s'élargir, entre les cheminements de notre pensée et le fonctionnement des machines qui nous aident à réfléchir comme à maîtriser le monde. Scandale, peut-être.  Mais quel prix faudrait-il payer pour refuser aujourd’hui de prendre les hélicoptères technologiques qui nous permettent de le franchir à mille heures du jour et de la nuit ? Renoncer à parler, dans un même corps langagier, pour ne pas dire une même discipline, des hommes et des machines, c’est tourner le dos à la cybernétique

On peut comparer l'opposition cerveau/IA à l'opposition oiseau/avion.

Malgré le nombre des chercheurs qui se sont intéressés à ces questions pendant les cinquante dernières années, ni les scientifiques ni les philosophes ne sont parvenus sur ces questions à des solutions définitives et convaincantes, tous appellent à la poursuite des recherches. Daniel Andler (in [Bloch 99]) conclut : Il reste à saisir la nouvelle figure qui émerge, sous nos yeux, de cette floraison de nouveaux sujets;».

Pour les humains, on pourrait disgintuer - une métrique organique : poids, consommation, pollution, coûts de conception, de formation, d'entretien pendant la retraite, criminalité (donc exige police et armée) et
-une métrique fonctionnelle: productivité, valeur pour les autres.
Mais est-ce bien sérieux ...

9. Qualitatif et quantitatif

Une solution intermédiaire consisterait à réserver le langage quantitatif aux sciences de la nature, et ne parler des hommes qu’en termes qualitatifs, qui préserveraient mieux sa transcendance. Mais ce serait encore abandonner une large part des sciences de l’homme. Psychologie et sociologie ne peuvent guère se développer sans mesures, au moins statistiques.

Poussant plus loin mes réflexions sur la digitalisation, je tendrais à formuler l’hypothèse : il n’y a pas de différence entre le quantitatif et le qualitatif. Les grandeurs elles-mêmes étant représentées par des bits, quand le système grandit il faut ajouter des bits. Cette distinction viendrait de notre mental, de nos catégories (kantiennes ?) subjectives, et non pas des systèmes digitaux eux-mêmes qui n’en ont que faire. Mais cette position est trop simpliste. On pourrait travailler ici à partir de la construction des nombres réels. Le qualitatif représenterait partirait du bit (qualitatif  égale à la base bon ou mauvais), puis une échelle d’entiers de plus en plus grand (affinement de l’échelle de qualité), et le quantitatif « pur » n’apparaît, avec la puissance du continu, qu’au terme d’une longue complexification (N, Z, Q, R). Et qui sait, peut-être pourrait-on faire la démarche inverse ?

Bref, je ne vois pas comment on peut parler de l’homme sans recourir à la machine, de multiples façons différentes, à moins d’en rester aux récits d’Homère, de la Bible ou de la Marabatha (ce ne doit pas être le nom exact).

Le constructivisme légitime au contraire le lancement de concepts indépendamment des intuitions de base et à en prouver la légitimité par la fécondité structurelle et par une réponse favorable de l’univers, interrogé à la lumière de ces concepts au moyen d’un appareillage expérimental (outils matériels de mesure et protocoles, c’est à dire encore des machines). Le concept est prouvé s’il marche bien. S’il tourne bien. Circularité, certes, mais aussi légitime que la fabrication de n’importe quel roue, dentée ou pas.

Au demeurant, le problème ne se pose pas dans un environnement statique. Actuellement les technologies du silicium progressent beaucoup plus vite que celles des neurones. Par leurs performances (loi de Moore basique) mais aussi par les parcs existants et l’ampleur des fonctions qui leur sont confiées. Par conséquent, de plus en plus,  l’homme sera évalué à l’aune des machines. Nous allons, sinon vers des post-humains, du moins vers un post-humanisme.  Ceci donne aux recherches sur la LHD, au delà de leur légitimité épistémologique,  une légitimité non seulement épistémologique, un intérêt pratique et éthique non négligeable. Mais bien entendu ouvert à la critique.

De là on débouche sur le post-humanisme.

10. De la LHD à l’IHD

La loi de Moore étant bien plus rapide que la loi de Leroi-Gourhan, cela conduit, en attendant une formulation mathématique plus précise, à considérer que le facteur de croissance est un facteur lui-même évolutif avec le temps.

La loi était   P(n+1) = i.P(n+1), avec i=2^1/2..

On a maintenant i = 2^2/3.

Pour Leroi-Gourhan, on a les valeurs successives : 2^1/50000, 2^1/32000, 2^1/6000, 2^1/1000.

On devrait donc pouvoir affecter un indice à chaque époque, l’IHD (indice historique digital). Il  caractériserait l’évolution des « technologies dominantes » à cette époque.

11. IHD et mesures économiques

L’IHD nous conduit naturellement à un rapprochement avec les séries chronologiques que nous fournit l’économie.

Car à chaque époque, on peut aussi déterminer, pour les différents technologies, et en particulier pour les technologies de pointe, significatives de l’époque, un « prix par bit ». L’IHD est en quelque sorte la dérivée seconde (ou la courbure) de ce prix historique. (Ici, il faut avancer dans la modélisation et les formulations mathématiques).

Or les prix peuvent jouer aussi bien au numérateur qu’au dénominateur de notre loi générale, et nous ramener aux bons vieux principes généraux des prix de vente, prix d’achat dont la différence donne le bénéfice… ou aux thèses les plus complexes sur la valeur. A la limite, la loi générale ne serait qu’une vue optimiste posant que le rendement du capital augmente exponentiellement avec le temps. Malgré l’enthousiasme actuel de la Bourse, cela semble un peu trop beau.

Quelques analogies peuvent nous encourager dans cette voie:

La monnaie est digitale par nature. Comme les autres machines digitales, elles se dématérialise au fil des ans.

Un tel rapprochement nous permettrait peut être d’avoir de nouvelles vues sur les problèmes difficiles évoqués par le paradoxe de Solow.

Mais surtout, une bonne modélisation nous permettrait de ramener dans notre modèle tous nos chiffres sur l’informatique, à partir du chiffre d’affaires des sociétés d’informatique, au niveau micro mais surtout macro-économique

Avant de conclure, relevons quelques points qu’il faudra préciser.

12. Le choix des granularités synchronique et diachronique

L’application de la LHD  ne peut se faire que moyennant un lissage, le choix d’une granularité matérielle et temporelle. Une technologie n’existe pas en elle-même, mais seulement par ses instanciations dans un certain nombre de machines concrètes, qui à un moment donné ne répondent qu’imparfaitement à son rendement théorique.

Une machine, ou un type de machine (Intel 8086) a une certaine durée de vie. Pour préciser la loi, il faudra dire quel date on prend : annonce de la machine, première mise en service, ou encore date de maturité, obtenue a posteriori en prenant le sommet de la courbe de succès, ou de maturité.

Une bonne généralisation de la loi suppose aussi que l'on prenne non pas une machine déterminée, mais une population de machine, avec ses propriétés moyennes caractéristiques.

La bonne granularité, en nombre d'exemplaires dans une population considérée comme uniforme, variera donc dans le temps. A nos époques de forte production, une population suffisante peut avoir une durée de vie de quelques années, quelques mois. Après quoi ce type est périmé. Aux époques préhistoriques, le cycle de vie des technologies se compte en milliers d'années. Noter qu'il y a des problèmes particuliers au moment du big bang, où au contraire les modifications structurelles se font dans des période de plus en plus courtes en tendant vers les point origine.

Problèmes: comment on date une machine (date de l'annonce, de la première livraison, de la moyenne de vie). Passer des nuages aux régressions. De même, pour les prix. Différences entre les prix catalogue, les prix réels, les machines d'occasion. 

13. Modélisation, explication, causalité

Une simple constatation et des mesures précises ne peuvent suffirent à satisfaire notre esprit. Nous aimerions comprendre le pourquoi de cette loi.

Quels sont les facteurs susceptibles de fournir une explication.

Un investissement en recherche permet de faire progresser la technologie. Il faut ensuite un investissement industriel pour atteindre les productions de masse, elles-mêmes nécessaires pour financer le cycle suivant.

A une période donnée, sont en interaction les facteurs suivants :

. un certain état des connaissances techniques, qui se communiquent par la documentation et la formation (par extension  : formation des jeunes mammifères supérieurs par leurs parents, transmission génétique, épitaxie...)

. une certain état des entités types et des entités les plus avancées

. des populations plus ou moins abondantes et plus ou moins en interaction

. de là découle une certaine aptitude au progrès, une certaine plus value, qui s'explicite par la recherche et le développement industriel (par extension : conquête de nouveaux territoires, acquisition de nouveaux comportements par les mammifères supérieurs, espace de mutations génétiques possibles, espaces favorables à l'apparition de molécules plus complexes).

C'est ici que l'on pourrait chercher à implanter une thermodynamique du digital: distance, masse, pression/température, densité…

On a d'abord des entités, dont la plus petite est le bit, la plus grande l'espace entier. Toute entité est le regroupement de plusieurs bits.

Chaque entité a son L.

Loi de Grosch (généralisée) : toutes choses égales par ailleurs, le rendement d'une entité est d'autant plus élevé que l'unité est grosse. Grosch avait posé, au départ, que la puissance croissait comme la racine carrée du prix de la machine. Mais on s'est aperçu par la suite qu'il ne s'agissait en fait que d'un choix tarifaire d'IBM.

Loi de Metcalfe (généralisée) : toutes choses égales par ailleurs, le rendement d'une entité est d'autant plus élevé qu'elle a des communications avec un plus grand nombre d'autres entités, et que ces relations sont riches.

Loi de Berger : Tout message entre deux entités doit être d'autant plus chargé que ces entités sont éloignées.

Loi de Gupta (généralisée, et d'ailleurs à vérifier) : Toutes choses égales par ailleurs, la combinaison de plusieurs entités comporte des charges de structures. Dans certains cas, ces charges croissent rapidement avec le nombre des entités, faisant tendre rapidement la puissance globale vers une asymptote (avec rendement décroissant de chaque entité quand le nombre augmente).

Loi de Gillier (généralisée. En ce sens, cas particulier de la loi de Gupta) : plus on unifie les descriptions d'univers, plus on augmente le nombre des dimensions. Et sous la simplicité apparente, plus se cachent des Laplaciens tordus.

Loi de Arthur Rock : le coût d’une "fab" (chaîne de fabrication) augmente de 50% à chaque génération. Les capacités augmentent aussi. Mais à la limite il ne sera plus possible de trouver des marchés suffisants pour une nouvelle fab.

Loi de Bellec : celui qui fait la dynamique des prix, c’est le second acteur

Notes sur la loi de Moore :
- SIA : une dialectique collusive, mais pas vraiment d’entente
- Histoire : « nuts and bolts » Vs. « social construction of technology » . nettement plus complexe
- Ceruzzi considère la loi de Moore comme un contre-exemple de social construction
- SIA, rapports annuels, avec dcision de ce qu’il faut faire pour qu’on tienne la loi de Moore. Parties faciles marquées en vert, parties « on ne sait pas comment » marquée en rouge.

On peut aussi définir des pressions sur les entités.

Dans la mesure où des entités existent dans un même espace, on peut parler de densité dans cet espace. (Un tel espace est-il une densité).

Relativité digitale : au delà d'une certaine dimension, les entités deviennent fragiles, instables, à la limite inviables.

14. Combinaison et succession des technologies

La loi ainsi généralisée permet donc de comparer et d’étudier les combinaisons de technologies.

Cela peut se faire :

. de manière synchronique : compétition entre technologies co-présentes dans un même biotope (ou technotope…), combinaison de couches technologiques au sein d’un même d’un même système (et tout particulièrement, bien entendu, technologies du silicium et technologies du carbone).

. de manière diachronique : succession darwinienne de technologies  accomplir des fonctions analogues ou pour occuper le même technotope.

14.1. Combinaison synchronique

L’analyse par niveaux part de l’observation de bases que l’opposition organe/fonction est en quelque sorte empilable, un peu comme les couches OSI en matière de réseaux ou les motivations dans la pyramide de Maslow.

Chaque niveau a besoin pour exister de disposer d’un certain nombre de fonctions (que dans une certaine mesure il met à la disposition de niveaux supérieurs) et exploite pour ce faire un certain nombre d’organes (qui lui sont en partie interne, voir ici éventuellement si on pourrait introduire une théorie de la sous-traitance, de l’entreprise étendue, du groupware ou de la sociométrie).

On peut par exemple, pour les systèmes digitaux,  proposer une série de 5 niveaux (on pourrait affiner en sept niveaux)

. physique, où la LHD s’applique en termes de bits par unité de matière/espace/temps,

. syntagmatique, où la loi se mesure nombre de bits par syntagme, densité syntagmatique du système),

. logique (et le seul à proprement parler digital), où la loi se mesure en nombre de bits utiles par rapport au total des bits, c’est à dire, en complexité descriptionnelle rapportée au nombre total de bits,

. langagier, se référant au rendement précédent mais perçu par un niveau supérieur du système

. transcendant, limite théorique de perfection d’un système, où les valeurs transcendantales (vrai, bien, beau) finissent par se réaliser à zéro-bit, ou comme dit Lamartine : « Ce bien idéal que tout être désire, et qui n’a pas de nom au terrestre séjour »).

14.2. Développement diachronique et successions

Sous l’effet de la compétition darwinienne, de la « main invisible » chère aux économistes et, qui sait dans quelle mesure, de l’intervention volontariste des hommes, de leurs instances de pouvoir (et peut-être aussi des interventions régulatrices de Gaïa, de Zeus ou de la Providence, sans oublier Shiva, Belzébub et autres puissances échappant à la matière comme à la digitalisation) les technologies ne font pas que co-exister, elles se succèdent.

L’évolution d’une technologie déterminée part d’une origine, pas toujours nettement tranchée (en particulier dans le cas de l’humanité, mais on peut en dire autant de l’informatique). A partir de là, elle tend à se répandre autant qu’elle le peut, et se heurte à des limites qui

. soit la stabilisent (courbe en S, je ne retrouve plus le nom) en elle-même, en quelque sorte isolément,

. soit la stabilisent en équilibre avec des concurrents dans son technotope,

. soit la font disparaître complètement, supplantée par une autre technologie de fonctionnalités radicalement supérieures.

Exemples plus ou moins classiques à étudier/mesure : Néanderthal et Cro-Magnon, micro-ordinateurs contre mainframes, mémorisation organisée (généalogistes africains) contre mémoires externes, électronique contre papier…

14.3. L’unification de la LHD par les lois de substitution

Une des formes d’unification de cosmologie et de (tentative de) démonstration de l’universalité de la LHD passe par l’élaboration de critères de substitution entre les technologies, notamment à fonctions égales. Ceci est indispensable si l’on veut utilement agréger les lois observées pour les silex préhistoriques, la montée de la métallurgie et en particulier des engrenages, la verrerie optique, l’électronique analogique puis digitale, tout autant que les machines logiques en elles-mêmes (en tant qu’indifférentes à telle ou telle forme d’implémentation, qu’elle soit neuronale (Aristote ou les scolasticiens enchaînant les syllogismes) mécanique (machine de Jevons), ordinateurs modernes en programmation classique ou de type IA (systèmes experts, CBR).

Nota. Piste d’analyse pour les engrenages. Au niveau physique, le paramètre intéressant est sans doute le poids (et les autres paramètres matériels) d’une dent. Problèmes :

. combien de dents pour une vis sans fin

. limites inférieures (une ? deux ? en pratique rarement moins d’une quinzaine. la gamme Meccano commence à 11 dents) et plus de 50 (maximum Meccano 133 dents)

. et surtout : combien de bits pour une dent ? On peut partir par le versant organique (nombre de bits opératoires pour fabriquer une dent en MOCN) ou fonctionnel (en partant de fonctions équivalentes dans les pendules ou les machines à calculer…).

15. Différentes catégories de limites

Ces limites peuvent provenir

. du versant organique : on bute sur les ressources disponibles en quantité (énergie, composants mobilisables, limites géographiques du technotope, temps disponible quant aux ressources humaines, fiabilité des machines, fautes et maladies des hommes, et bien entendu… budgets) ;

. du versant fonctionnel,  le niveau supérieur ne peut pas consommer plus d’unités fonctionnelles : « il y a trop d’informations », la machine est trop compliquée, charge mentale, saturation du processeur de niveau supérieur (par exemple dans une architecture CIM, saturation du marché.

On dépasse ces limites soit par passage à une technologie complètement nouvelle, soit par une nouvelle « génération » d’une technologie déterminée. La frontière entre les deux mutations n’est pas toujours d’une grande clarté, et peut combiner la continuité à un niveau et la rupture à un autre. Par exemple, l’arrivée du micro-processeur n’est guère qu’une mutation technologiquement (au sens de l’électronique) presque insensible par rapport aux chip-sets précédents (UAL, registres, circuit de contrôle…).  Mais, à un niveau plus « macro », le micro-ordinateur et la micro-informatique ont constitué culturellement et économiquement un saut quantique, une révolution considérée comme telle, à tort ou à raison, par ses acteurs.

16. Un cas classique, l’interface homme-machine

Dans le cas particulier des machines utilisées par les êtres humains, le problème se poser régulièrement sous la forme suivante. Pendant un certain temps, la machine se perfectionne de manière en quelque sorte homothétique entre sa complexité fonctionnelle et sa complexité organique. On ajoute à la fois des composants nouveaux et des fonctionnalités nouvelles. Un peu comme on achète de nouveaux objectifs pour son appareil photo ou qu’on apprend de nouvelles techniques pour travailler, de nouvelles positions pour l’amour ou de nouvelles poésies pour se les réciter au clair de lune.

Vient un moment où la complexité fonctionnelle (c’est à dire ici la complexité de l’interface vue du point de vue de l’utilisateur humain) dépasse les capacités mentales (en statique ou en dynamique) de l’utilisateur. L’ergonomie permet de repousser un peu les limites, mais pas indéfiniment. On peut aussi (recommandations d’Oehmichen) décomposer les commandes en deux panneaux, un accessible par l’utilisateur normal, l’autre réserve aux experts, régleurs et opérateurs de maintenance (ces commandes sont placées derrière l’appareil ou à l’intérieur du carter).

Quand cela ne suffit plus, il faut faire prendre une partie des commandes en charge directement par l’appareil. Autrement dit remplacer des boucles ouvertes par des boucles fermées. Et là on fait un saut (topologique, puisqu’on établit des boucles) qui découple la croissance en complexité fonctionnelle de la croissance en complexité organique.

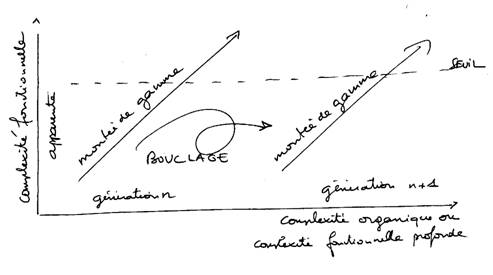
On atteint encore un niveau supérieur avec les propositions de l’université de Valenciennes (voir notamment la thèse de Mourad Abed, 9/1990) où l’on demande à la machine elle-même de régler le niveau d’opérations qu’elle laisse à l’opérateur afin de s’adapter à sa charge mentale.

17. De l'histoire à la prospective

Du descriptif, la LHD doit nous conduire à rechercher des modèels explicatifs, et de la, à des projectdiosns fur l'avenir.

18. Notes d'après Gérard Dréan, au séminaire de Pierre Mounier-Kuhn

Séminaire Histoire de l'Informatique : historiographie, méthodes et sources. P.-E. Mounier-Kuhn, CNRS - 2009-2010. 2  décembre:  La "loi de Moore": un cas réductible de déterminisme technique ?

Liens :
www.ahti.fr (ou www.get-telecom.fr/ahti)
www.feb-histoire.com
http://www.histoireinform.com/
http://www.aconit.org
http://www.computerconservationsociety.org/links.htm
Fondation Mémoires Informatiques
http://www.memoires-informatiques.org
http://www.irisa.fr/chir2004
http://www.asti.asso.fr/index.html
http://www.paris4.sorbonne.fr/article.php3?id_article=1164#04
http://www.laurent-bloch.org/article.php3?id_article=13
Site consacré aux instruments de calcul: http://linealis.org…et, pour ceux qui s'intéressent aux relations de l'informatique avec l'art :
http://lutecium.org/stp/FRED.html

Bibliographie

[Boehm 82] Barry Boehm : Software Engineering Economics. Wiley, 1982.
[Bloch 99] Vincent Bloch (sous la direction de) : Cerveaux et machines. Institut Fredrik Bull. Hermès, 1999.
[Ceruzzi 98] Paul E. Ceruzzi : A History of Modern Computing. MIT Press, Cambridge,Massachusetts,  1998.
[Chaline 99] Jean' Chaline, Laurent Nottale et Pierre Grou : « L'arbre de vie a-t-il une structure fractale », in Comptes-rendus de l'Académie des sciences, 15 juin 1999. Cité par Le Monde du 3/9/1999.
[Christensen 97] : Clayton M. Christensen : The innovators Dilemma. Harvard Business School Press, Boston, 1997.
[Debeir 86] Jean-Claude Debeir : Les servitudes de la puissance. Flammarion 1986.
[Delahaye 99] Jean-Paul Delahaye : Information, complexité et hasard. Hermès 2^e édition 1999.
[Dhombres 98] Jean Dhombres, article « Nombres réels » in Dictionnaire des mathématiques, volume « Fondements, probabilités applications », Albin Michel 1998).
[Leroi-Gourhan 65] A. Leroi-Gourhan : Le geste et la parole. Tome I. Technique et langage, 1964. Tome II. La mémoire et les rythmes, 1965. Albin Michel.
[Virilio] Paul Virilio. Le grand accélérateur. Galilée 2010.
[Volle 00]Michel Volle : « Evolution du prix des micro-ordinateurs » in Revue de Marne-la-Vallée, Juin 2000 ( ?)