L'informatique libère l'humain
2. L'âme digitale émerge du monde.
L'automate, système élémentaire
Développements ultérieurs (en anglais) sur les entités digitales (digital beings).
Nous disposons maintenant d’une mesure générale exprimant la « valeur » d’un système binaire, aussi bien pour ceux qui entrent en relation avec lui que pour le système lui-même. Il a « tout intérêt » à maximiser cette valeur L, quel que soit le degré de conscience qu’il puisse prendre de lui-même.
Cherchons à mieux comprendre comment cette valeur peut s’intégrer à un fonctionnement qui représenterait, sinon la vie, au moins l’existence, l’activité, les relations d’un système avec son environnement. Le modèle classique des "automates finis" peut nous y aider.
Reprenant un terme proposé par Alain Lioret, nous avons tenté une formalisation sous le terme Being, relations entre beings avec des développements sur les aspects génératifs .
La liberté dans une boîte noire
Rappelons qu'un automate fini peut être représenté comme une "boîte noire" fonctionnant de manière cyclique. Il comporte une entrée, une sortie et une mémoire. Chacune de ces parties transporte ou stocke un certain nombre fini de bits. A chaque cycle, l'automate exécute une fonction S : (O,E) = S (I, E) . (Nous utilisons I pour input et O pour output, mais gardons E pour état, puisque S représente déjà le système). Les bits émis en sortie et le nouvel état sont déterminés par les bits reçus à l'entrée et des bits de l'état précédent.
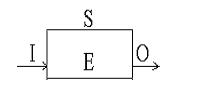
Précisant notre modèle, en ce qui concerne les états successifs du système, on pourrait considérer que le processus même de reproduction d'un instant à l'autre est décrit dans E. Mais cette hypothèse ne va pas sans problèmes et n'est pas indispensable.
La fonction S peut être considérée comme un programme. D’ailleurs l’expression que nous en avons donnée est plutôt celle d’une instruction d’affectation qu’une fonction mathématique proprement dite, qu’il serait plus correct d’écrire avec des indices i et i+1 pour I et E, S restant non indicé puisque sans changement au cours des cycles successifs.
Ce programme S accepte des données en entrée (I), sur lesquelles il n’exerce aucun contrôle, et qui donc peuvent a priori être consi-dérées comme parfaitement aléatoires. Il tient compte de ce qui figure dans sa mémoire (E) pour calculer aussi bien les sorties (0) que pour déterminer (mettre à jour, si l’on veut) le nouvel état de sa mémoire.
L’universalité du digital nous permet d’aller plus loin. En effet, un programme n’est qu’une suite particulière de bits. Il peut donc être stocké dans E. Nous pouvons donc considérer cette mémoire E comme composée de deux parties : A (comme algorithme, pour faire image) , portant le programme S, et D (comme données) pour ce qui n’appartient pas à A.
Nous ne pouvons tout de même pas nous débarrasser totalement de S, car les programmes contenus dans A doivent s’exécuter sur un processeur, qui ne peut être décrit complètement par le programme lui-même. Mais nous pouvons admettre, et la réalité de l’infor-matique le confirme, que l’on peut définir un processeur minimal, que nous considérerons donc comme présent à la racine de chaque automate fini. Appelons-le R (comme racine). Alors, A se décompose en R et F (comme fonctionnement), F représentant les fonctions spécifiques à l’automate S. R comprend notamment les fonctions de recopie du système sur lui-même d’un instant à l’autre.
Nous en tirons deux conséquences :
1. Comparaison possible entre S. Deux automates ne diffèrent que par l’ensemble de F et D, ou plus formellement par la chaîne binaire concaténant F et D. Cela permet toutes sortes de comparaisons, la plus simple étant la longueur de cette chaîne. Toutes choses égalespar ailleurs, la chaîne la plus longue désigne le système le plus perfectionné, le plus complexe. Cette chaîne binaire représente la partie H de notre fonction d’autonomie L. On verra par la suite comment peut s’exprimer la partie P.
2. Non étanchéité de la coupure entre F et D. La frontière entre programmes et données n’est pas étanche. Rien n’empêche même que le système reçoive, par son entrée I, de nouveaux programmes, qui prendront la place des programmes anciens ou empièteront sur l’espace disponible pour les données.
Le sens comme effet de I sur l’automate
Le sens, c'est aussi le résultat que produit le message sur son récep-teur, humain ou mécanique, et ce qu'en fait le récepteur. Le fait qu'il exécute l'action prévue prouve qu'il a bien compris le sens du message. "Au pied, le chien". "Veuillez livrer dix tonnes de ferraille à notre entrepôt du Havre". De ce point de vue, les machines perçoivent le sens des messages aussi bien que les animaux et les hommes. Des millions de fois par seconde, un microprocesseur exécute les ordres que lui transmet l'utilisateur par son clavier ou qu'il prend à la suite dans son programme.
Le message peut n'avoir aucun effet extérieur immédiat (0). Son interprétation peut se traduire uniquement par un stockage enmémoire (modification de E), ou même, simplement, la valeur reçue étant normale, il n'y aucune action à lancer. Pour autant, il aura fallu que la machine extraie d'un message parfois long (une image de caméra, par exemple) quelques bits "significatifs" et en tire les conséquences.
Universalité de l'automate fini binaire
Les systèmes binaires peuvent tout faire. Un bit peut indiquer à la machine qui le lit une action élémentaire, lui donner le choix entre deux possibilités: allumer la lampe verte ou la lampe rouge, faire ou ne pas faire telle action : allumer un radiateur, ouvrir une porte, fermer une vanne. Avec un groupe de bits, le nombre d'actions possibles augmente autant qu'on veut. Et le jeu des opérations s'étend de la même manière que celui des représentations, relayé si nécessaire par des "convertisseurs digital-analogique" qui rempla-cent une chaîne de bits par une tension continue, et par des ampli-ficateurs pour augmenter la puissance, aussi bien pour forcer le son de la chaîne audiovisuelle que pour commander de gros moteurs ou des vérins hydrauliques.
Mais le bit peut aussi représenter l'état d'un phénomène extérieur, ou d'un résultat précédent obtenu par la machine et, par là, déclencher ou choisir une action en fonction de conditions exté-rieures ou préalables.
Pour agir et pour faire, la machine enchaîne des opérations. Ici intervient un dispositif binaire essentiel: l'horloge. Ce simple circuit passe de 0 à 1 à intervalles réguliers, en pratique, très vite (aujourd’hui plusieurs centaines de millions de fois par seconde). L'horloge est en quelque sorte le seul "moteur" des systèmes binaires. C'est elle qui entraîne tous les autres circuits de la machine, mais plutôt comme un chef d'orchestre que comme la machine à vapeur du siècle dernier qui faisait tourner toute l'usine. L'horloge donne le rythme, un rythme, un élan purement formel, purement digital. L’énergie au sens propre, physique, est fournie par l'alimentation électrique de l'ensemble, le plus souvent par un générateur de courant continu bien stabilisé.
Ainsi s'est développé le modèle fondamental de toutes les machines informatiques d'aujourd'hui. Mis au point dans les années 40, il n'a pour l'instant jamais été supplanté, malgré de nombreuses tentatives. Dans ce schéma, un jeu d'instructions (additionner, soustraire, transférer de l'information...) décrit les actions possibles, comme les pièces d'un Meccano. On les combine sous forme d'un programme, c'est-à-dire d'une suite d'instructions placées dans le bon ordre. Certaines instructions sont "conditionnelles" et interrompent la lecture séquentielle pour repartir à un autre endroit du programme. C'est le fameux "IF... GO TO ...".
Ce schéma n'est pas très compliqué, mais il suffit à tout. Et les circuits électroniques qui le réalisent se construisent aujourd'hui par dizaines de millions chaque année.
Structuration de E
Pour les données comme pour les programmes, et de manière conco-mitante, le progrès va se traduire tantôt comme un allongement des chaînes binaires, tantôt par une montée en complexité de leurs struc-tures, une organisation plus efficace. Il serait peut-être possible de construire abstraitement une théorie montrant comment cette montée en complexité se développe, comment, par exemple, l'opposition entre opération et opérande peut polariser progressivement l’ensemble du champ de E. Si elle est possible, cette théorie reste à faire. Contentons-nous de quelques exemples, inspirés tantôt des systèmes vivants, tantôt des ordinateurs d’aujourd’hui.
Premières structurations: tramages, typologie élémentaire
Pour que les fonctions puissent opérer sur quelque chose, il faut qu’elles sachent où trouver leurs opérandes, qui sont une partie de la chaîne binaire constituant D. Le moyen est de donner une adresse à chaque bit de la chaîne.
Dès que D est grand, cette adresse est relativement longue (loga-rithme à base 2 de la longueur de D). Par ailleurs, peu d’opérations s’adressent à un bit isolé, de signification réduite (oui/non). La plupart portent sur des chiffres, des caractères. La première structu-ration vient du groupement de bits en petites unités, capables de désigner différentes opérations ou opérandes. Historiquement, l’informatique a fini par donner un rôle tout particulier aux groupes de 8 bits, alors que le code biologique de l’ADN comprend quatre racines chimiques.
Ce tramage s'étend tout naturellement à l'ensemble de E (aux pro-grammes et pas seulement aux données) et le plus souvent aux entrées sorties I/O, bien que nombre d'effecteurs et de capteurs ne soient que des points "tor" (tout ou rien), donc se suffisant d'un seul bit. Ce tramage, et a fortiori la diversification des tramages, exige une montée en complexité des fonctions F (on peut peut-être admettre que R reste au niveau des bits élémentaires et ne tient pas compte des tramages). Le tramage suppose par exemple qu’à partir de l’adresse de début, les fonctions sachent compter le nombre de bits de l’opérande pour opérer correctement.
Assez naturellement, chaque zone sera affectée d’un type, indiquant le type d’opérations que l’on peut lui appliquer. Dans les systèmes simples, ce type est implicite. On suppose que les opérandes indiqués par une addition vont pouvoir effectivement être additionnés. L’expérience de la programmation montre qu’il s’agit d’une source importante d’erreurs. Les langages évolués permettent donc de "typer" les opérandes et de vérifier au moment de la compilation du programme que les types correspondent bien aux opérations prescrites.
L’espace E va donc se "tramer" en séquences d’une certaine longueur (mots) et, en pratique, en une hiérarchie de longueurs, comme la page, ou le gène dans le monde biologique. En effet un simple tramage, de longueur fixe, est limité.
Si la trame est courte, la signification de chaque mot est réduite (256 valeurs pour un code de 8 bits). Pour construire différents niveaux de longueur, on peut soit adopter des longueurs fixes (comme les enregistrements d’un fichier en longueur fixe ou, par analogie, les différents types d’atomes, dont les dimensions sont comparables). Mais, en longueur fixe, plus on allongera les mots et plus le rendement baissera, car il manquera des parties pour compléter un nombre croissant d’enregistrements.
Réciproquement, une trame binaire très longue (plusieurs millions de bits) ne convient en général que pour des signaux continus ou pour la représentation d’une image. En effet, ici encore, le rendement baisse avec la dimension, car il y a de grandes plages de blanc, de silence ou, plus généralement, de valeur constante.
Compression et codification intelligente
Pour améliorer le rendement, le système recourt à deux types de techniques : la compression et la codification sophistiquée. Toutes deux exploitent des régularités observées dans les paquets ou flux de données binaires, des répétitions ou des relations plus ou moins faciles à observer, mais qui en tout cas permettent une réduction des volumes de données en les traduisant au moyen de méthodes appropriées.
La compression opère sans se poser de questions sur la nature des objets représentés ou des opérations à effectuer. Elle se contente de statistiques. L’observation d’un texte, par exemple, montre que la fréquence d’utilisation des différentes lettres est très variable. Un texte français, par exemple, comporte beaucoup plus de e que de w. Il peut donc être intéressant d’utiliser des codes courts pour les lettres fréquentes, plus longs pour les lettres rares. L’observation d’une image permet le plus souvent de repérer de longues plages de même couleur. Plutôt que de répéter deux cent fois « bit blanc », il est avantageux de dire une seule fois « deux cents bits blancs », à charge de les décompresser quand un programme les utilise. Cela complique bien sûr les programmes et allonge leur exécution.
Donnons quelques exemples. L’informatique utilise des algorithmes de compression. Le biologique fait sans doute de même avec ses mémoires de différents types. Dans la vie courante, le classique « Rien à signaler » est une forme de compression qui évite de répéter à chaque instant la totalité des observations faites quand elles sont identiques à celles de l'instant précédent.
La codification intelligente, au contraire, s’appuie sur la nature même des opérations qu’entend effectuer le système ou sur les pro-priétés des opérandes. Elle « met en facteurs » les parties identiques de ce point de vue. Les données de base sont représentées par un produit : type x caractères spécifiques. On peut ici multiplier les exemples : bases de données, programmation objet, codes de fichiers avec en-têtes. On peut aussi rappeler l’organisation d’autres types de mémoires, notamment les archives sur papier avec leur hiérarchie classique (caractère, mot, phrase, paragraphe, chapitre, volume, ouvrage, rayon, bibliothèque...). La complexité des données en D va de pair avec un accroissement de complexité des programmes. Un fichier simple peut être traité par des machines simples, des machines à cartes perforées, par exemple. Une base de données relationnelle exige (et encourage d'ailleurs) des outils plus puissants. Une base de connaissances de type système expert est encore plus exigeante.
Construction d'un modèle du monde
Le perfectionnement d’un système porte de manière corrélative sur ses opérandes et sur ses opérations, sur ses programmes et sur ses données. Chez les êtres humains, le perfectionnement des langages, des théories, de la science, va de pair avec une meilleure description des objets du monde. Le problème même de la vérité peut se poser ici en termes pratiques, sinon même quantitatifs : un nouveau concept, une nouvelle théorie, est utile si elle permet de mieux décrire l’univers, soit en conservant la même quantité d’information mais sous un volume réduit, soit en ayant plus d’information avec la même puissance du système.
La quantité d’information inclut ici la fiabilité de cette information. Une théorie est plus vraie qu’une autre si les prédictions qu’elle permet sont plus souvent confirmées par l’observation.
Il ne s’agit pas ici de prendre une position métaphysique sur la réalité du monde dans l’absolu, qui réduirait toute l’épistémologie au constructivisme. Cela ne revient au même que dans la mesure, toujours limite, où nous pouvons modéliser les processus de connaissance par les automates finis.
Il y a probablement une limite à ce type de construction, et sans doute elle pourrait se calculer. Il vient un moment où l’accrois-sement de complexité n’est plus possible ou n’a plus d’intérêt. Le produit types par caractères spécifiques atteint un maximum, que nous pourrions appeler la « racine carrée » expressive de notre ensemble E. Cela doit correspondre, en quelque manière, au moment où l’on est le plus proche de l’équiprobabilité de tous les bits (ou de toutes les valeurs que peut prendre l’ensemble de bits).
Le texte, au coeur de l'âme digitale
Il faut ici faire une place particulière au texte et à cette limite du texte qu’on appelle "langue naturelle". On peut en effet considérer que le système s’organise de manière de plus en plus tramée, de plus en plus régulière, au fur et à mesure que l’on s’éloigne du cœur (de la partie en relation avec le matériel, nous le verrons plus loin).
A l'opposé, près du cœur, de la racine R, le système a une organi-sation subtile, indifférenciée et plastique comme un embryon, riche de potentialités non développées, et par là même apparaissant de l’extérieur comme "non structuré".
Dans le monde des représentations digitales, le texte représente tout particulièrement cette plasticité déroutante. Les automates finis, par construction, sont déjà fortement structurés et entièrement digita-lisés, ce qui ne permet pas du tout la grande plasticité, le flou même, de la « langue naturelle », encore largement plongée dans le corporel, en permanence en état d’émergence par rapport à l’inconscient et aux cris inarticulés de la vie animale voire minérale.
Un programme est déjà une catégorie de texte hautement formalisée. L’intéressant est que ses couches partent de formalismes pauvres, émergeant eux aussi à peine de la matière du processeur (le langage machine) pour aller vers des formalismes de plus en plus riches. Nous avons tendance à penser que la montée en niveau (du "langage machine" aux outils du génie logiciel) se fait par rapprochement progressif du langage humain, de la langue naturelle. Un très grand nombre de gens, y compris des informaticiens, ont l’impression que tout sera résolu le jour où ils pourront parler à leur ordinateur, comme si, alors, il devenait totalement transparent pour eux, faisant la synthèse parfaite entre la disponibilité de la machine-esclave et la complicité avec un autre homme, établissant une sorte de communication immédiate, pour ne pas dire de communion.
En fait, la machine progresse, son langage aussi. Et il y a des raisons de penser que notre langage naturel n'est pas un optimum absolu. Bien au contraire, si les machines progressent, elles élaboreront pour converser entre elles, voire avec elles-mêmes, des langages qui seront de plus en plus étrangers aux nôtres. Cependant, et pour longtemps encore, l’homme représente une telle capacité de complexité active et positive que les ordinateurs auront « tout intérêt » à savoir converser avec lui.
Le sens et les valeurs
Voir réflexions ultérieures sur le bien, le vrai, le beau
Orientation dans l'espace des états
Un bit isolé n'a pas de sens. Il faut un autre bit pour lui en donner.
- Soit l’autre bit se situe à son niveau, formant chaîne avec lui. Alors le sens de chaque bit découle de sa position dans la chaîne : bit de poids fort, bit de poids faible. Comment le savoir, d'ailleurs? Le sens ne s'impose de lui-même que si la chaîne est assez longue pour que son interprétation elle-même ne puisse se faire que dans une seule direction. C'est du sens "sémantique" de la chaîne que découlera le sens "spatial" à choisir pour la lire.
- Soit le bit se situe à un autre niveau, en position métalinguistique par rapport au premier et indiquant à l'opérateur quelle est la convention choisie. Il indique, par exemple qu'une tension positive indique une valeur numérique 1, ou la valeur logique "vrai", et qu'une tension négative représente une valeur numérique 0, ou la valeur logique "faux". Cela dit, si le bit métalinguistique est accolé au premier dans le message, on est ramené au problème précédent. Et de toute façon, comment savoir quel code a été choisi pour la signification du bit métalinguistique lui-même ? Dans tous les cas, donc, le sens d'un message binaire ne se trouve finalement que par sa signification même, quand il est assez grand pour que la place qu’il prend dans le système des représentations lui donne de soi l’interprétation qui convient.
En revanche, à l'intérieur d'un système binaire déterminé, l'orien--tation une fois choisie doit être constante pour tout le système, de même que la nature a choisi, une fois pour toute, les sucres qui virent à droite (ou à gauche, je ne sais plus, et peu importe).
Les valeurs
Au fur et à mesure que le système se différencie, on peut commencer à considérer aussi que L lui-même, comme expression de valeur, peut se différencier de différentes manières. L traduisait de manière bidimensionnelle la valeur propre à l’être, aux êtres existants. P exprime la survivance dans l’être (l’existence est la première des perfections, disent les scolastiques). H représente la richesse de l’essence et de ses propriétés à un moment donné.
Dans un automate différencié, on peut voir émerger le modèle des "valeurs", aussi bien pratiques et techniques que celles tradition-nellement appelées "transcendantales" : le bien, le vrai, le beau.
Le bien, c’est un programme qui tourne bien, sans erreur. Un bon objet est celui convient à un programme à un moment donné, qui a le bon type.Le vrai, ce sont des données qui ne génèrent aucune contradiction ni entre elles, ni avec les entrées, ou des entrées qui ne génèrent pas de contradiction avec les mémoires.
Le beau, enfin, c’est une bonne correspondance, un bon équilibre, entre données et programmes. Et au sein même des données comme des programmes, les caractéristiques du beau selon la scolastique, qui ici prennent tout leur sens : l'intégrité (il faut que rien ne manque ; ou, plus finement, le mot même d’intégrité tel qu’il est repris, par exemple, dans les systèmes de bases de données), la clarté (le programme ne doit pas perdre son temps à transformer des structures mal faites dans les données ou dans des sous-programmes pour poursuivre son fonctionnement) et, bien sûr, couronnement du tout, l'harmonie, avec ses déclinaisons quantitatives et qualitatives.
Le sens comme reconnaissance
Mais le sens n'est-il pas, pour nous humains, bien autre chose que l'exécution d'un ordre ? Mots et phrases ont du sens pour nous dans la mesure où ils évoquent en nous des images, des émotions. Les images ont du sens car nous y reconnaissons des objets connus ; nous décodons les expressions des visages... Nous comprenons ce que le message, ce que notre interlocuteur, "veut dire", son intention. Nous les voyons dans notre tête, ou dans nos rêves. Cela encore peut se modéliser, avec les hiérarchies de mémoire, les niveaux de reconnaissance, etc.
Montée en complexité des structures internes
La montée de ces structures fait apparaître, au sein de notre auto-mate fini, des sous-automates. Montrons pourquoi.
Tramage du temps
D’abord la structuration même du temps y conduit naturellement. Si notre automate exécute un programme sur ses données (mémoires plus données en entrée), il faut bien admettre qu’il y a des sous-cycles permettant l’exécution du programme. S’il fallait n’exécuter qu’une instruction de programme à chaque cycle, cela reviendrait finalement au même, mais il faudrait considérer comme des sur-cycles les passages d’un programme à un autre et, à l’intérieur d’un sur-cycle, il faudrait en pratique interdire de nouvelles entrées, sous peine d’aboutir à une situation chaotique.
Il y a donc aussi un tramage du temps. Et il est logique, en se combinant avec le tramage de notre chaîne E, que nous finissions par découper des pavés dans cet univers à deux dimensions. Ces pavés sont des sous-automates, des sous-systèmes. Une de leurs caractéristiques est que leurs entrées et leurs sorties se font à l’intérieur même du système, sauf pour certains sous-systèmes particuliers qui ont précisément pour vocation d’assurer les liaisons du système avec l’extérieur.
On peut tenter une première typologie des sous-systèmes de liaison :
- à l'entrée : filtres, analyses, simples affectations à la mise à jour de mémoires, à la confirmation de la situation de non-danger, ou au contraire émission d'alertes vers le niveau supérieur, délocalisation des données ou abstraction ;
- à la sortie, générateurs, "synthèse" des sons, images, etc. localisa-tion de l'action, concrétisation dans l'ici-maintenant.
D’où l’émergence d’une typologie des processeurs : certains sont surtout orientés vers la communication avec l’extérieur (I/O), d’autres sur la mémorisation (E), d’autres sur l’exécution de pro-grammes (A, B, R... ci-dessus), et les programmes qui sont autour d'eux, gardent leur indifférenciation.
Certaines formes de réflexion conduisent à passer au travers de ces différentes typologies. La programmation objet, par exemple, repose en principe sur l'association, au sein d’un même objet, de ses données et de ses fonctions.
Plus précisément, le programme lui-même crée des classes, avec des instructions de programmes et des types de données. C’est au moment seulement de l’exécution du programme que l’objet est instancié et que les données deviennent de vraies données.
La distinction entre organe et fonction semble a priori liée à la matérialisation. En fait, l'opposition peut se décrire de façon pure-ment logicielle, avec des processeurs, surtout s'il s'agit d'automates infinis.
La fonction d'un sous-système consiste à effectuer un certain nombre de tâches, à jouer un certain nombre de rôles que lui délègue le système. Sous l'angle fonctionnel, le système ne s'intéresse pas à E ; c'est essentiellement ce qui est obtenu en sortie qui intéresse le S plus général. Un processeur comme l'horloge est un pur fournisseur de bits en sortie (implicitement, tous les S subordonnés ont une entrée d'horloge qui déclenche leurs cycles). Pour d'autres fonctions, les bits d'entrée qui intéressent le système sont uniquement des
"bits de contrôle" (qui lanceront des fonctions, par exemple des requêtes en mémoire. On n'exploite que E). D'autres processeurs ont au contraire des fonctions de travail sur des flux, par exemple les filtres en entrée, les synthétiseurs en sortie.
Un sous-système apparaît comme organe dans la mesure où il occupe une certaine place dans le système général et consomme un certain nombre de ressources. Cette nécessité va de soi quand les systèmes sont matérialisés. Mais elle s'impose tout autant dans les systèmes purement digitaux à partir du moment où la consom-mation d'un espace binaire se paye toujours quelque part, du fait de la relativité. On peut modéliser, dans un univers purement digital, indépendant de toute "incarnation" particulière, la compétition pour l'occupation de ces ressources binaires abstraites, ou encore les concepts de surface blanche, de ressource libre, énergie fluide, etc.
Une part importante du progrès de l'organisation des systèmes consiste précisément à optimiser l'affectation des bits disponibles pour maximiser l'efficacité des organes et l'efficacité globale. En particulier : bons groupements, bonne granularité, bonne corres-pondance entre fonctions et organes. On ouvre ici la voie à une étude des relations entre le L de chaque organe et le L général.
Nous voyons donc apparaître une "géographie" ou "anatomie", même à l'intérieur de systèmes purement abstraits, digitaux, indé-pendamment de toute matérialisation.
La boucle, l’autre
La structure la plus apparente est hiérarchique. L'espace se répartit en zones, organes ou fonctions. Mais une autre type de structure vient compléter la hiérarchie : la boucle. Une grande partie de la réflexion organisationnelle et du montage adéquat des structures entre entités vise, par nature profonde ou par volonté explicite, l’organisation hiérarchique. Une autre partie doit être consacrée aux différentes formes que peuvent prendre les boucles, ces structures essentielles (mais souvent déroutantes) pour la vie des systèmes.
C'est notamment la structure en boucle qui donne sa consistance au principe "tout ce qui est formalisable est automatisable". Du point de vue digital, la boucle ouverte, qui laisse les décisions à un intervenant extérieur et la boucle fermée, où la décision est prise par le système lui-même, sont très proches l'une de l'autre. Il suffit que l'instruction "IF" trouve ses conditions dans un registre interne, de valeur aléatoire à la limite, ou dans un capteur fourni par "la nature", au lieu de la trouver dans un ordre donné par un opérateur, par un bouton ou un dispositif quelconque.
Ainsi peut apparaître, au sein même de l’automate fini, un sous-automate disposant d’une certaine autonomie par rapport à lui et dont on peut aussi calculer la fonction L. Le développement des automates finis peut donc être considéré comme une évolution récursive (sous réserve du fondamental R).
Ainsi peut aussi apparaître "l'autre". D’abord s'affirme une certaine consistance du « monde extérieur », par le fait que les entrées I sont largement répétitives. Puis vient le moment où le système est capable de prendre en compte le fait que ses actions O ont des effets qu'il peut percevoir en I. Si ces effets sont totalement déterministes et a fortiori s'ils sont obtenus dans le même cycle, on peut purement et simplement remplacer les bits I correspondants par des bits E.
En général, c'est plus compliqué. Le système commence alors à modéliser l'extérieur comme il est lui-même, c'est-à-dire un ensemble auquel il envoie des O et qui lui ramène des I. Et il cherche à modéliser un système S' (monde extérieur) avec :
I' = O (ou I' contient O)
I = O' (ou I est contenu dans O')
et des états intérieurs E' que l'on cherchera à déterminer (modéli-sation) pour construire les formules :
O' = f' (I', E')
E' = g' (I', E')
Pour construire ce système de manière efficace, S cherchera à bloquer les entrées de S' de telle sorte que I' ne comporte pas d'autres bits que ceux venant de O (ce qui revient à dire qu'on étudie S' "toutes choses égales par ailleurs").
Comme pour l’univers intérieur, la structuration de E’ conduira à distinguer différents sous-processeurs dans le monde extérieur, etc. S pourra aussi s’apercevoir que son propre fonctionnement, ses propres structures, ne sont pas sans ressemblance avec celles de certains sous-ensembles du monde extérieur. Il commencera alors à se percevoir comme une partie du « monde » et à étoffer en son sein les représentations de lui-même :
- dans E, mémoire de soi, mémorisation des états du passé, prévision de l'avenir, théories psychologiques mises en mémoire ;
- dans I, cénesthésie ; dans un univers purement digital, la perception des états internes ne rend pas nécessaires des capteurs au sens propre, mais des raisons d'efficacité conduisent à avoir des résumés des états, ce qui finalement revient au même ("moniteurs hardware", sondes logicielles) ;
- dans I encore, image de soi par l'extérieur : miroir, psychologie constructiviste, actions explicites de connaissance de soi par l'extérieur : génération de I pour avoir amélioré E.
Il y a une sorte de dialectique, de pulsation dans les structurations. Tantôt une entité grandit, augmente son H, ses fonctions E,I,O, son rayonnement en quelque sorte, les fait croître de manière stric-tement « quantitative ». Tantôt, quand le nombre devient grand, le rayonnement se structure jusqu’à former de nouvelles molécules, de nouveaux systèmes.
Prise en main progressive du système par lui-même
Nous pouvons alors apporter une première réponse à une question qui se pose implicitement quand on étudie cette organisation pro-gressive ou ces différents degrés d’organisation des systèmes : comment un automate peut-il passer d’un état à un autre, plus perfectionné ? Un système peut d’abord être passif. Il est changé de l'extérieur. A ce niveau, tout objet peut être considéré comme un automate : une action sur lui (I) donne des résultats (O).
Par exemple il réfléchit des rayons lumineux. Et il a aussi un certain état (E) : température, vitesse par rapport au monde extérieur, dont l’évolution dépend des actions I comme de l’état actuel E. A ce stade, il n’y a pas à proprement parler de cycle, mais un observateur extérieur pourrait en introduire artificiellement un par projection de son cycle propre (voir plus haut, modélisation du monde extérieur par S).
Le système devient un automate fini de manière intéressante à partir du moment où l’agent extérieur peut le modéliser comme tel et agir sur lui comme tel, notamment en modifiant son comportement de manière à proprement parler digitale, c’est à dire en agissant sur des entrées I et par elles sur son état E.
L’automate sera de plus intéressant pour un agent extérieur au fur et à mesure de l’enrichissement de ses fonctions I, E, O, et notamment à partir du moment où on pourra le programmer, c’est-à-dire modifier son comportement de manière stable et utile par l’intermédiaire de ses entrées I.
Le système va devenir un automate encore plus perfectionné s’il devient adaptatif. C'est le cas, en particulier, quand il commence à pouvoir piloter ses fonctions O de manière à recevoir des entrées I de plus en plus intéressantes (maximisation de H) et, le cas échéant, quand il dispose d’une fonction plus ou moins élaborée d’évaluation de P et des résultats que ses O ont sur son P.
On peut introduire ici une notion de « profondeur d’adaptation », suivant le niveau de fonctions que S peut changer en lui-même, suivant qu’il peut se rapprocher plus ou moins profondément de son R… S’il pouvait maîtriser la totalité de R, il serait Dieu.
Généralisation à l'univers entier, totalité des processeurs
Nous avons vu que la structuration naturelle d’un système, quand on étudie des niveaux de complexité de plus en plus élevés, conduit à l’apparition de sous-processeurs, de sous-systèmes. Pourquoi alors ne pas poser que tous les automates finis que nous décrivons ne sont que des sous-automates d’un automate «général », qui pourrait être une première idée de notre « âme digitale » ?
L’automate général a alors une propriété particulière : il n’a pas d’entrées ni de sorties, et sa fonction est donc simplement E = S(E). Les fonctions d’entrée et de sortie concernent ses sous-automates, sont des échanges entre ses sous-systèmes.
Ainsi l’univers digital tout entier pourrait se trouver décrit par une longue chaîne digitale, le E de l’automate général… mais il subsisterait le problème des moyens d’exécution de R, car ici on ne peut même plus faire l’hypothèse d’un système extérieur.
L'augmentation d'autonomie d'une entité, sa montée en complexité et en durée de vie se fait tantôt aux dépens d'autres entités, qui sont capturées, absorbées, fusionnées, assimilées, ou simplement détruites pour récupérer leurs matériaux utiles ou pour dégager l’espace. Mais elle se fait aussi par coopération, par win-win, et donc par construction de relations de plus en plus élaborées. Il s'agit en particulier de choisir la "bonne distance" entre entités.
Cela se conçoit aussi bien dans la vie minérale (distance des atomes dans les molécules), végétale et animale (densités de population dans un biotope), psychologique (distance nécessaire entre un ménage et ses beaux-parents) que purement digitale, avec ses distances et surtout dans les modèles relativistes ici évoqués.
En effet, l'existence autonome d'une entité quelconque suppose que règne suffisamment de "non-structure" autour de ses frontières pour que l’environnement n'apporte pas de perturbations trop fortes. Cela est à combiner avec le prix imposé par la structuration en unités autonomes avec leurs organes de synchronisation.
Le problème difficile qui reste à résoudre est celui de la combinaison des L de différentes entités quand elles coopèrent. Quelques réflexions ont été conduites sur ce point, pour montrer par exemple que l'assurance profite à l'assureur comme à l'assuré ou, en informatique industrielle, par la théorie de la commande distribuée. Nous allons proposer ici un cadre général qui pourrait permettre l’étude de cette question.
La conception d'un système global de ce genre risque de buter sur un certain nombre de difficultés et de paradoxes analogues à celui de "l’ensemble de tous les ensembles". Et c’est sans doute un bien, en tout cas du point de vue des non-réductionnistes.
Tentons alors de dépasser le modèle des automates finis et de leurs assemblages bien déterminés pour réintroduire le chaos et les interstices nécessaires à notre psychologie humaine, pour prendre en compte les limites de la logique en elle-même et, au-delà d'elle, les contradictions de notre psychologie et le chaos du monde matériel.