L'informatique libère l'humain
L'informatique libère l'humain. 2. L'âme digitale émerge du monde.
Pour une théorie générale du digital
Développements ultérieurs (en anglais) sur le digital.
Les bits n'existent pas dans la nature. Nous, ou nos machines, les y imprimons pour y exprimer nos conceptions et nos décisions. Les bits ne sont que l’expression d’une volonté explicite. Mais, une fois matérialisés, objectivés, ils échappent à la volonté de celui qui les a émis. Les bits sont une négation de la nature, une coupure dans sa continuité. Mais, une fois posés, ils nient leur auteur. Non seulement ils subsistent après l'acte qui les a fait naître, mais ils s'organisent entre eux. Ils constituent par leur combinaison une "complexité" qui exclut de leur cercle même leurs créateurs.
Voir sur ce point d'abondans développements dans notre texte sur les bits.
La nature ne se plie pas volontiers, ni avec une parfaite souplesse, à cette volonté. Nos idées, ou les représentations que nous en formons en nous ou sur des supports extérieurs, ne la représentent pas par-faitement. Nos décisions sont toujours un peu "à côté de la plaque". L’action de nos machines n’est jamais totalement fiable, totalement adaptée.
La nature, c'est précisément ce qui n'est pas l'effet, direct ni indirect, de nos décisions, ce que nous n'avons ni choisi ni construit et qui, donc, n'est pas digital. Tout ce qui est digital est voulu, donc arti-ficiel et réciproquement, au moins dans une certaine mesure.
Le digital proprement dit a été préparé par les quinze milliards d'années de coupures et d'organisation qui ont conduit à l'homme. Mais cette description est très anthropocentriste. C'est nous qui décrivons ainsi cette histoire. C'est moins de mille ans avant le Christ que l'auteur du premier chapitre de la Genèse raconte la création sur le mode digital des séparations et des constructions progressives. C'est au XIXe siècle seulement que la logique, puis le calcul font la théorie du binaire, au milieu du XXe que la puissance unificatrice de ces conceptions se matérialise dans des machines efficaces et vraiment digitales et à la fin de ce même siècle que la numérisation s'étend à toute la planète et à tous les ménages ayant passé le seuil du téléphone ou de la télévision.
Ayant retracé cette longue histoire dans la première partie, tentons maintenant de formuler les principes permanents qui s'en dégagent aujourd'hui et nous fournissent les axes de construction de l’avenir. Cette construction essaie de libérer de leurs attaches anthropo-morphiques un certain nombre de concepts comme la liberté ou le sens. Elle vise une description purement digitale. Ce ne peut être qu'une esquisse, d'abord parce que son élaboration demanderait un long travail de formalisation mathématique aussi bien que de relevés quantitatifs dans le monde "réel", ensuite parce que les limitations même de l'esprit humain tel qu'il est actuellement lui donnent un caractère temporaire, relatif. Malgré ces limites, qu'elles soient accidentelles ou fondamentales, cet essai espère relancer le travail quantitatif dans des domaines considérés comme relevant de la philosophie, c'est-à-dire d'une mise en texte qualitative.
Le miracle digital
Les systèmes digitaux sont universels, puissants, efficaces. Miracle? Le mot est un peu fort. Mais on n'hésite pas à vanter les beautés d'un cristal, d'une plante, de la vie, à s'étonner que le hasard de l'évolution des planètes ait ouvert dans le système solaire un petit espace, la Terre, où la vie peut s'épanouir, malgré l'infime probabilité, la quasi-impossibilité statistique d'une telle chance. Certains se laissent émouvoir par la beauté d'une formule mathématique, d'une élégante démonstration ou du bourgeon-nement coloré d'un système fractal. Alors, pourquoi ne pas chanter les beautés du monde digital ?
L'Evangile lui-même recommande cette radicale simplicité: "Que votre discours soit oui, oui, non, non". Les templiers, dit-on, possé-daient une tête d'or qui répondait à toutes les questions et résolvait tous les problèmes par une suite de oui et de non. Ces moines, ou ceux qui ont créé leur légende, pressentaient donc la logique binaire ; ils sentaient déjà la force de ces oppositions franches. Les logiciens grecs avaient déjà formulé la loi logique du "tiers exclu". A leur suite, les philosophes et théologiens du Moyen Age feront du "distinguo" l'une des armes favorites de leurs discussions.
Il a fallu l'explosion du calcul électronique, des ordinateurs, pour porter jusqu'au grand public les vertus des systèmes numériques, désormais présents sur la plupart des chaînes haute-fidélité, demain sur les téléviseurs et les appareils de photo familiaux.
Hélas ! les autorités terminologiques françaises ont choisi de tra-duire l'anglais digital par numérique, confondant ainsi le chiffre (digit) avec le nombre (number, ou figure). Distorsion regrettable dans son principe et dans ses conséquences psychologiques : elle réduit à la numération un mode d'expression, sinon d’existence, beaucoup plus général.
Nostalgies et mauvais procès
Le système binaire dérange. La variété des oppositions ou des réserves qu'il suscite confirme d'ailleurs son universalité. Des psychologues, et même certains psychanalystes, contestent son caractère brutal, qui serait incompatible avec les finesses de notre conscience ou la véritable libération de notre inconscient. Pourtant, dès que l'on utilise un nombre suffisant de bits, les nuances les plus fines peuvent s'exprimer de manière digitale, jusqu’au-delà de nos capacités sensorielles. Ces réticences prolongent la vieille méfiance des littéraires à l'égard des scientifiques.
Des philosophes, moralistes ou théologiens y voient un retour au manichéisme, cette doctrine médiévale, une des racines du mouve-ment cathare, pour lequel les hommes et les choses ne pouvaient être que radicalement bons ou mauvais. Le même reproche s'applique à toute phrase, déclaration ou maxime un peu courte. Il faut un peu de temps, ou de longueur, pour exprimer les finesses d'une philosophie et prescrire des attitudes éthiques à la mesure de l'homme et de sa complexité.
Des logiciens, même, chantent les mérites des logiques ternaires: oui, non, je ne sais pas (ou "peut-être"). Or il suffit d'ajouter un deuxième bit pour exprimer cette nuance ou, plus finement, pour qualifier l'affirmation contenue dans le premier, voire plusieurs bits, pour indiquer un degré de probabilité, ou mieux encore, remplacer les points noirs et blancs par des taches moins nettes, grâce aux "ensembles flous". Au niveau des circuits électroniques, une logique à trois états s'avère parfois utile. Mais il s'agit simplement de dispositions locales simplifiant la construction des composants, sans en changer le fonctionnement théorique. Même les spécialistes de la théorie de l'information font remarquer que trois serait plus près que deux du nombre e , qui serait un optimum théorique.
Plus radicalement, les systèmes analogiques éveillent toujours des nostalgies. Au lieu de découper les représentations en bits, pourquoi ne pas construire et manipuler des formes et des dispositifs continus, de forme analogue aux phénomènes repré-sentés ? L’expérience montre qu’on ne peut aller loin dans cette voie. Le digital s'impose par son efficacité pratique, la précision théoriquement illimitée qu'il permet et d'autres aptitudes que nous verrons plus tard. Mais l'analogique résiste bien, et même parfois reconquiert des domaines qu'il avait perdus, quand il s'agit de faire communiquer les humains avec les machines: retour des aiguilles sur les montres et pendules, voyants expressifs sur les tableaux de bord de voitures, icones sur l'écran des ordinateurs. Cela ne remet pas en cause la supériorité du digital dans le fonctionnement des machines elles-mêmes, ni dans leur communication entre elles.
La liberté, mesure universelle
Le monde binaire peut aussi se mesurer indépendamment des corps chimiques où il s'incarne, qu'il s'agisse de la chair au sens biologique, des circuits de silicium ou des surfaces optiques et magnétiques. Mieux, il trouve en lui-même des limites et des structures, plus importantes et plus profondes sans doute que celles, accidentelles ou conjoncturelles, que lui impose la chimie. Le plus simple est d'abord, bien entendu, de compter les bits, ceux que portent chaque dispositif ou ceux qui sont nécessaires pour décrire un dispositif, donc exprimer sa complexité, et la totalité de tous les bits, peut-être, sous réserve (à étudier) que l'on ne bute pas ici sur un paradoxe analogue à "l'ensemble de tous les ensembles".
Osons mesurer la liberté !
La liberté peut se définir négativement, comme une non-dépendance. Mais cela ne prête guère à la mesure, en tout cas directement. Tentons donc une approche plus frontale. La formule proposée peut s'appliquer à tout système, mais mieux encore aux systèmes digitaux pris en eux-mêmes. Nous verrons ensuite comment cette formule peut se mettre en relation avec les supports matériels et les positions psychologiques.
Dans un premier sens, la liberté désigne une capacité autonome de choix et peut donc s'évaluer comme la variété des choix possibles pour le système à un moment donné. Un homme ou un système est d'autant plus libre qu'il a le choix entre des actions, des paroles, des déplacements, des expressions différentes. Les choix se multiplient rapidement par combinaison de choix élémentaires, et il est donc souhaitable de mesurer leur nombre par l'intermédiaire de leur logarithme. Si l'on prend un logarithme à base 2, la variété se voit en pratique ramenée à un certain nombre de bits. La liberté implique aussi que l'on puisse choisir entre les différentes possibilités de la manière la moins contrainte possible, autrement dit que les états soient équiprobables. Cela se mesure aussi, et la variété cède la place à une mesure meilleure, la néguentropie (H).
Mais, pour avoir une liberté de choix, encore faut-il que le système existe, soit en état de fonctionner. En ce sens, on parle de l'autonomie d'un dispositif portatif pour exprimer le temps qu'il peut fonctionner sans recharger ses batteries ou ses réservoirs de carburant. Plus généralement, l'autonomie mesure une "durée de vie indépendante".
On peut combiner ces deux mesures en additionnant la néguentropie du système à tous les instants de son existence, après avoir affecté chaque instant de la probabilité que le système a de survivre à cet instant futur. On obtient ainsi une fonction que nous appellerons L, pour liberté. pt représente la probabilité que le système existe à l'instant futur t ; le reste de la formule représente sa néguentropie à cet instant (pour être plus exact, il faudrait rajouter un signe moins):
|
Voir réflexions ultérieures sur cette formule de la liberté
On ne prétend pas que cette formule exprime la liberté dans toute la profondeur et la transcendance de cette valeur pour l’homme. Mais elle permet d'esquisser un certain nombre de calculs et donc de mieux comprendre comment la liberté "fonctionne" en pratique, et d'orienter ensuite notre action pour la défendre et la promouvoir. En particulier, elle exclut l'idée que la liberté est une et simple, qu'on est "libre" ou "pas libre", que "la liberté ne se divise pas". Bien au contraire. La liberté est en permanence le résultat d'un effort de construction mais aussi d'un arbitrage, entre le court et le long terme, entre l'égoïsme et l'altruisme, entre le sensuel et l'intellectuel.. Il faut noter que le temps se présente ici comme une succession discontinue d'instants, et sans référence aux unités courantes, celles du monde "physique" (seconde, année).
Un approfondissement de ce point conduit à travailler sur la complexité.
Une présentation graphique de L
Repartons de notre formule L et représentons-la graphiquement en la combinant avec le modèle des automates infinis. L'état présent forme une ligne de bits que l'on peut comparer à un nombre écrit en base deux mais, pour faire image, que l'on peut aussi bien penser en base dix.
invariants "poids forts" "poids faibles" instables
![]()
Ceux qui sont les plus à gauche sont les plus stables. Ils constituent la structure permanente du système, par laquelle il persiste dans l'être. Pour une valeur numérique, ce seraient les chiffres les plus à gauche, les bits de poids forts. Au bout d'un certain nombre, on s'arrête. Mais cet arrêt ne serait que relatif si l'on plaçait le système dans un environnement plus vaste. Par exemple, si ce nombre re-présente la position du système dans le monde, ce pourrait être sa longitude, en partant du méridien de Greenwich. Il y a un nombre de bits finis. Mais si l'on voulait avoir une position par rapport à l'ensemble du système solaire, il faudrait rajouter à droite un certain nombre de bits qui représenteraient la position de la terre par rapport au soleil, et ainsi de suite.
Les bits les plus à droite sont les moins stables. A partir d'une cer-taine distance par rapport au "centre", disons "de la virgule" pour un nombre, les chiffres perdent même leur signification. Dans l'exemple de la longitude, on peut la donner à quelques mètres près. En dessous du décimètre, cela ne veut plus dire grand-chose, car mon corps est plus grand et, en outre, comporte des parties mobiles les unes par rapport aux autres.
Il en irait de même pour une mesure physique, une température, par exemple. Ici, à gauche, nous atteignons assez vite une limite en nombre de chiffres, car nous butons sur le zéro absolu. A droite, les chiffres perdent assez vite aussi leur signification, soit que l'on arrive aux limites de précision des instruments de mesure, soit que l'on tente de donner une température précise à un corps dont les différentes parties sont à des températures différentes.
Graphiquement, nous pouvons imaginer que la première ligne de bits que nous avons dessinée représente l'instant présent. Juste au
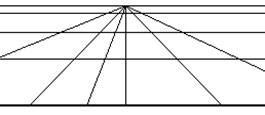
dessus, une deuxième ligne représente l'instant suivant, et ainsi de suite. Pour faire image, on peut tracer ces traits de plus en plus près les uns des autres, et se confondant de plus en plus dans un effet de perspective qui conduit à l'horizon. Vus "du point de vue de Sirius", les états sont équidistants ; mais, du point de vue de l'opérateur, ils ne se distinguent que dans un horizon proche. Et les état passés sont "derrière", ils ne sont plus visibles. Nous retrouvons sur cette dimension du temps un peu la même répartition que pour les bits d'état: un certaine période seulement de temps est effectivement perçue par le système.
On pourrait aussi faire un modèle circulaire (polaire), en supposant un centre autour duquel le système, ou tout l'univers, tourne. Au centre, transition sans aucune erreur. Inconvénient, l'instant a la forme d'un angle...
La liberté, sens de la vie et orientation de l'action
Qu'entend-on, quand on parle de "faire du sens", de "donner un sens à sa vie"? Cela consiste à recevoir ou à se donner un certain nombre de "valeurs" qui permettent de choisir ce que l'on fait, avec de grandes décisions (comme le choix d'une carrière, d'un conjoint, d'une postérité) et des décisions mineures qui s'y inscrivent (faire tel voyage, lire tel livre, manger ici ou là, à telle ou telle heure, mettre tel vêtement ou tel autre). Si ma vie a un sens, au moment d'une décision je pourrai classer les alternatives (relation d'ordre) et donc choisir celle qui va le mieux dans le sens de ma vie.
Parfois cette relation d'ordre découle d'un processus rationnel, s'ex-prime même dans des nombres (comparaison du prix de différents produits identiques par ailleurs). Parfois, au contraire, ce clas-sement reste largement intuitif, émotionnel, quitte à la limite à sembler irrationnel (l'amour a ses raisons... c'était lui, c'était moi). Le problème de savoir comment on parvient à cette relation d'ordre en présence d'une masse d'informations de tous ordres a fait l'objet de travaux variés : recherche opérationnelle, analyse multicritères...
L'accroissement de notre autonomie peut et doit suffire à orienter notre vie. Et cete objectif n'est pas l'apanage de l'homme : pour tous les systèmes, le seul bien, c'est la liberté, à condition de lui donner une définition élargie, comme celle que nous avons proposée avec notre fonction L, avec ses charmes et ses limites : tantôt elle se traduit clairement dans les faits et les options, tantôt elle relève du risque ou de l'appréciation subjective.