Un algorithme de la liberté
N'étant pas mathématicien, il va de soi que la proposition faite ici, si elle présente un intérêt, devrait être développée et, si je peux ainsi dire, plongée dans un espace plus élégant que celui des formulations qui sont à ma portée.
Qu'est-ce donc que la liberté? C'est la "possibilité de faire ce que l'on veut", ce qui se peut se détailler plus précisément.
1°) On n'est libre que si l'on existe. Ventre affamé n'a pas d'oreilles. La liberté est liée à la possibilité d'exister dans une certaine plage de temps s'étendant vers l'avenir.
2°) On est libre à la mesure de la "quantité de choses que l'on peut faire", ou du "nombre d'états" (au sens d'état d'un shstème) que l'on peut choisir pour le présent et pour l'avenir.
3°) On est libre si l'on dispose d'une certaine indifférence vis à vis de ces états: on n'est pas déterminé, ni par des contraintes externes, ni par une fatalité interne, à faire telle ou telle chose.
4°) La liberté se joue sur la totalité de l'existence temporelle du sujet. Ce qui compte, ce n'est pas seulement ma liberté aujourd'hui, mais, pendant les années qui me restent à vitre. Et le plus longtemps possible, bien sûr.
Je propose de synthétiser tout cela dans une formule comme/
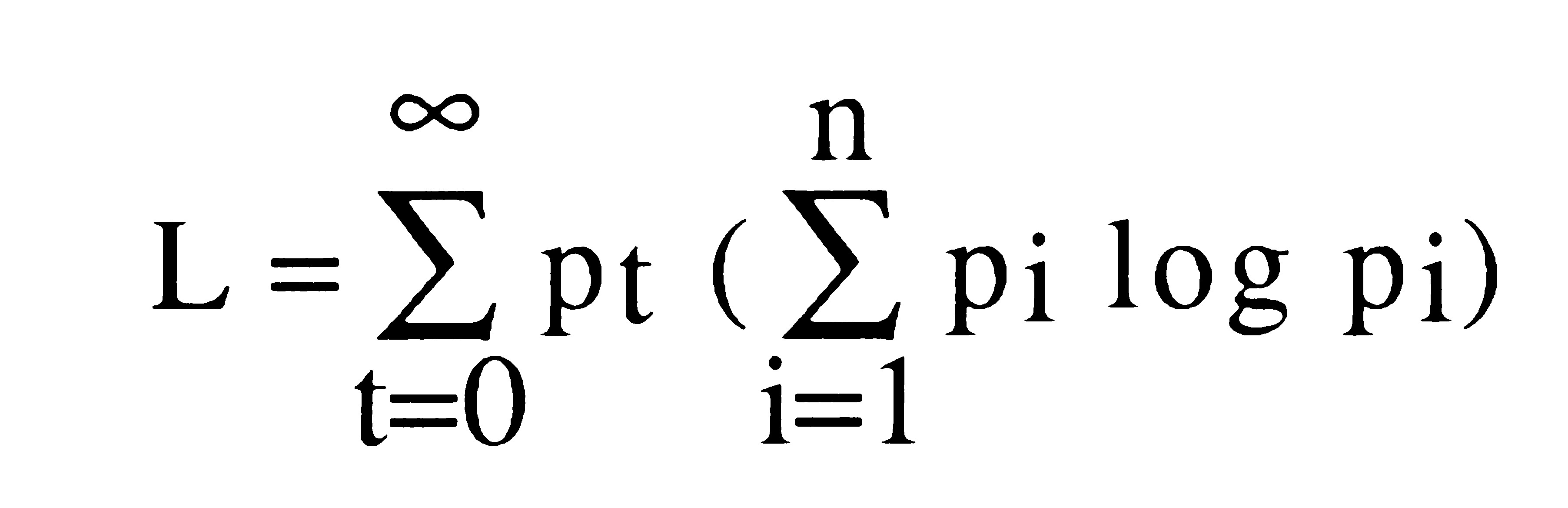
*1/1/2000. A l'époque où j'ai saisi ce texte, j'avais laissé en blanc. C'est seulement aujourd'jui que, et avec l'aide de Marcel, je maîtrise assez le traitement de texte pour intégrer une telle formule.
en prenant les partis suivants:
- on suppose que le sujet a une existence discrète pouvant se ramener à une suite d'instants t commençant à l'instant à venir et se terminant avec la disparition du sujet;
- on suppose qu'à chaque instant t le sujet peut prendre un nombre i d'états différents;
- p indice t est la probabilité d'existence du sujet àl'instant t
- p indice it est la probabilité qu'il a - s'il existe- d'être dans l'état i.
Cet algorithme n'est guère élégant. Il suppose un découpage du temps et un dénombrement des états possibles quelque peu arbitraire. Des formulations plus générales pourraient sans doute être proposées. Sous cette forme discrète, elle présente l'avantage de permettre un rattachement aisé à la théorie des automates.
Notons un certain nombre de points qui nous paraissent marquer l'intérêt d'une formulation de ce type.
Ambivalence de la liberté
L peut être accrû de trois façons différentes
- en accroissant p indice t, probabilit d'exister, c'est à dire en pratique sa longévité; cela exprime clairement que l'existence est la condition fondamentale de la liberté;
- en accrfoissant i, c'est à dire le nombre des états possibles pour le système, la liberté croit avec le nombre des choss que l'on peut faire;
- en accroisant l'équiprobabilité des états, l'indifférence, le libre arbitre du sujet.
Cette variété de moyens exprime de façon intéressante la liberté fondamentale du sujet: il peut arbitrer entre sécurité et aventure, entre puissance et maîtrise de soi, etc.
Base quantitative pour une typologie.
La formule permet tout de suite de différencier des sujts selon la prédominance de tel ou tel facteur.
La suite d'instants t est plus longue pour un sujet jeune que pour un sujet âgé. Les échelles de valeur diffèrent pour le "laboureur sentant sa fin prochaine" des hiérarchies de ses enfants.
Certains sujets choisiront le court temre en attribuant une valuer au p indice des petites valeurs de t; d'autrez, en sedonnant une courbe très différente pour p indice t, travailleront pour le long terme.
Les sujets craintifs sacrifieront l'accroissement de i à l'accroissemnet de leur longévité.
L'anarchiste ou le stoïcien mettront en avant l'indifférence, la gratuité de l'acte, en cherchant avant tout l'équiprobabilité des états i.
Des rapprochements avec les caractérologies classiques doivent être possibles.
Les optima ne sont pas aux extrêmes.
In medio stat virtus. Se présentant comme une somme de produits, la formule choisie pour L sera certainement défavorable aux choix trop orientés sur la pure longévité ou la pure liberté.
La formule présente un caractère très synthétique. Par le membre Somme... elle rattache la liberté aussi bien à la théorie de l'informtion qu'à la thermodynamique, en si situant très précisément à leur jointure. Par le membre pindicetelle ramène aisément à certains problèmes des mathématiques financières: il suffit de prendre pour p indice t une formule du type
1/ (1 + tau)puissance t
pour se ramener à un taux d'actualisation.
De plus, la formule choisie pour L présente une analogie frappante, mais que bien sûr il faudrait analyuser de plus près, avec la forme
Delta E. Delta t tilgé h
des relations d'incertitude de Heisenbert. Il serait évidemment très satisfaisant pour l'esprit de rarracher la liberté au sens général de l'indéterminisme atomique. Mais est-ce vraiment possible? (note 92: ceci est en partie fait par Eccles dans son libre de neurologie cérébrale).
(attention, ici il y a des iconos à reprendre)
Par ailleurs, présenté comme coefficient d'incertitude, la formule permettrait peut-être une certaine formalisation d'analyses sociologiqus comme celles de Michel Crozier sur les univers administratifs.
Il faudrait analyser la signification de dL.
Il faudrait décomposer les états possibles en grands champs, synchroniques et diachroniques. Si l'on suppose les états définis par des longs mots, binaires par exemple, on peut proposer une représentation du genre:

Le champ d'application est très large.
On peut appliquer la formule L à tout système. Elle exprme assez bien l'idée d'autonomie d'un système mécanique. Elle exprime des libertés spatiales (y compris dans le continu, car là il ne doit pas y voir de problème pour une expression "entropique" des libertés dns l'espace). Elle exprime assez bien l'intérêt de supports d'énergie polyvalents: l'essence peut servir aussi bien à ce chauffer (ce qui, en hiver, est favorable à Pindicet) qu'à se déplacer (ce qui accroît le nombre d'états spatiaux possibles). Etc.
Au delà de la liberté, la formule peut être considérée comme une base pour une théorie générale de la valeur.
Notons que d'assez nombreux jeux, notamment les échecs ou les dames, peuvent être consideérés comme une recherche -contradictoire- par les deux partenaires, d'une liberté maximale. La victoire est atteinte quand, l'autre n'existant plus, pindicet deivent égal à 1 pour toute valeur de t. L devient alors infini pour un joueur immortel.
Exemple: le coût de la sécurité. Mr. Chesneau (Informatique et Gestion no 42) établit la courbe suivante:
(icono)
On voit ici comme l'argent apparaît comme une bonne expression synthétique pour L. En sacrifiant une part de liberté: on dépense moins donc on peut moins investir, par exemple. On gagne de la liberté: le système existera plus longtemps, ou sera intègre plus longtemps.
On retrouve les voies de choix des systèmes mis en lumière par exemple en automatique, où à chaque niveau (voir l'article de Louis Richaud, Informatique et gestion janvier 1973) joue le triangle coût/performance/fiabilité. On voit clairement que L représente en quelque sorte le produit peformanc (somme pit log pit) * fiabilité (pt).
Un inconvénient important: la formule ne distigue par l'aléatoire du volontaire.
Aux objecteurs humanistes
Malgré l'application de plus en plus fréquente des mathématiques aux sciences humaines, il y aura peut-être des gens pour se scandaliser de voir mettre la liberté en équation. On peut les rassurer. La formule choisie laisse place à la subjectivité; elle devrait permettre tout à la fois de donner une face mesurable à la liberté tout en préservant son caractère transcendantal.
La subjectivité s'exprime par l'intervention des probabilités.
On sait qu'il s'agit d'une notion quelque peu paradoxale et difficile à formaliser dès que l'on sort de l'univers fréquentiste. Autrement dit, s'il est facile de bien cerner de quoi on parle quand on traite de la fréquence d'apparition du 4 quand on lance un dé un grand nombre de vois, il n'en va pas de même pour l'affectation de coefficients de probabilité à des événéments uniques, non répétitifs.
Par ailleurs,il s'agit de la probabilité pour un observateur. Pour un même sujet, L peut prendre des valeurs différentes selon qu'il s'agit des probabilités perçues par le sujet ou par un observateur. Le sujet peut se croire libre alors qu'il est en fait déterminé. Il peut, au contrare, faire preuve extérieurement, même pendant une longue période ou selon de nombreux points de vue, d'un comportement déteministe; et pourtant préserver une liberté intérieure qu'il fera éclater au grand jour au moment qui lui paraîtra opportun.
Ce caractère paradoxal des probabilités peut être considéré comme une limite à l'intérêt de la formule. On a prétendu mesurer, mais comment le faire en pratique sérieusement? Que veut-dire une formule qui mesure potentiellement très longtemps à l'avance des probabilités de tel ou tel état, alors qu'on ne sait guère ce que, en fait, sera le sujet à ce terme et ce que signifierait alors pour lui les états que l'on recense à la date de la mesure.
A cela deux réponses:
1) en prenant pour pt une valeur judicieusement dégressive en fonction de t, c'est à dire en prenant par exemple un taux d'actualisation suffisamment élevé, l'importance dans la formule des termes éloignés sera rendue aussi petite que souhaitable;
2) s'appuyer sur ce paradoxe des probabilités pour développer une théorie assez radicalement nouvele est peut-être la bonne solution à la fois pour sortir du paradoxe et pour développer quelque chose d'intéressant.
La notion même d'état distinct doit être analysée de plus près. S'il est facile pour une machine de Turing de décompter les états possibles, il n'en va pas de même pour les sujets complexes et en particulier pour l'homme. Le nombre des étas possibles est évidemment astronomique e luer recensement une idée purement abstraite. On procèdera en pratique par découpage, au sein d'un référentiel de possibles, des champs probabilistes, ou des familles d'étas susceptibles de se prêter à la mise en formule. Et sans pouvoir mesurer le L global, on pourra étudier ses variations en fonction de telle ou telle décision, toutes choses étant supposées égales par ailleurs. Cela correspond à une modélisation d'une partie du sujet, utile et propice à la mesure, mais ne mettant nullement en cause sa transcendance à toute
modélisation.
Enfin, bien entendu, une optimisation globale de L supposerait une élucidation complète des relations entre les deux aspects existence/entropie, ce qui ne paraît guère possible, hors bien entendu les modélisations.
Il faut surtout soulever un point fondamental. tout sujet connaissant se constitue en lui-même une certaine image de l'univers extérieur: c'est être dans deux états différents que d'imaginer un échiquier vide et un échiquier chargé de pièces. Le sujet pensant peut donc augmenter son L par simple développement de son univers intérieur. Dans une certaine mesure, le mystique, par exemeple, pourrait dire avoir atteint un L infini par connaissance du Dieu infiniment libre et varié. Mais peut-on placer les états cognitifs sur le même plan que les états "existentiels"? Cela mérite réflexioin, mais nous conduit à des réflexions usr la dynmique des systèmes qui montreront que notre formule n'est pas si éloignées que cela des préoccupations des informticiens.
Le complexe et le répétitif
Quelques réflexions décousues autant que complémentaires.
Le développement de la liberté L implique la constitution de réserves. Cela apparaît intuitivemnet à partir de la formule et de la nécessité de l'indifférence. Comme nous le verrons ailleurs, le problème est de savoir comment le sujet peut faire vrier L. Un des moyens fondamentaux est d'agir sur ses interfaces, réels ou virtuels, avec son environnemnet, de façon à pratiquer des échanges bénéficiaires.
(note 92: interface avec la réalité virtuelle).
Mais, de toutes façons, il faut avoir des "réserves" qui permettent, au moment opportun, d'affecter de l'énergie au poient où elle sera utile.
(note 92: l'écoute, une sorte de réserve, comme le papier blanc).
L'énergie libre se présente comme un objet simple et hautement répétitif. Ce seront des molécules d'essence, des phases de courant électrinque, des rotations du volant cinétique, de la graisse, de l'eau, du travail "qui n'a pas de sens" ou de l'argent qui n'a pas d'odeur. L'essence, flujide et sans
personnalité, et l'argent, devenant une valeur de plus en plus abstraite, illustrent au mieux cette idée. La matière est réduite au pur nombre, la structure n'apparaissant que comme un artifice secondaire mais indispensable "pour le moment".
Ce n'est jamais tout à fait le cas pour l'information. On cherche sans doute à lui donner une structure hautement répétitive dans les banques ou bases de données. Mais tout à la fois on élimine soigneusement les redondances pour les limiter strictement aux impératifs de la fiabilité. Le rôle du vocabulaire et de la syntaxe visent précisément à organiser la répétitivité des symboles pour permettre, aussi économiquement que possible. C'est pourquoi on dit que le mathématicien est paresseux.
La répétitivité joue un rôle essentiel. On a insisté sur le caractère répétitif des opérations pour en garantir une rentable automatisation. On oublie de signaler que cette possibilité de dire de plusieurs objets "c'est la même chose" est la base de toute la conceptualisaion, de toute la causalité. Et, bien entendu, de toute la science expérimentale, dont le critère essentiel est que l'expérience peut êter répétée.
On arrive à l'économie maximale, pense le théoricien, quand on arendu compte de la réalité par une structure unique que multipolie un nombre (cardinal).
Mais, en réalité, pour que tous les objets soient rattachés à une structure unique, il faudrait que cette structure soit infiniment complexe. Il sagit donc, en quelque sorte, d'optimiser la puissance de la structure par le nombre.
En matière informatique, cela veut dire que, à la limite, un programme infiniment complexe pourrait rendre compte, appuyé sur une base de données infinie, de la totalité du réel. C'est purement théorique. En pratique, il faut construire des programmes viables, exécutables un nombre raisonnable de fois.
Les structures elles-mêmes constituent une réserve. Le monde atomiquue le montre bien. E= mc2. Et le passage de l'un à l'autre est donc sous réserve d'un coefficient énorme.
Ces remarques, si leur fondement pouvait être explicité, sont la cause fondamentale de la convergence vers un système unique. Mais l'explicitation montrerait sans doute aussi pourquoi cette convergence est dialectique et, dans une certaine mesure, toujours niable, de même que la liberté.
Complexité rejoint variété dans l'opposition au répétitif. Le propre de l'automate, au sens classique, c'est qu'il reproduit toujours la même séquence. C'set très bien exprimé par Elsa Triolet dans "L'ame". C'est d'ailleurs par le nombre des séquences différentes que l'on définit le nombre d'état d'un automate.
On notera d'ailleurs qu'un calculateur fini ne peut générer que des nombres pseudo-aléatoires en chaînes identiques... est liée à la capacité de mémoire disponible. De même, le calcul d'un grand nombre de décimales d'un irrationnel comme pi trouve une limite dns la taille de la machine qui le calcule
L et les interfaces
Le meilleur moyen pour un sujet, et peut-être le seul, de modifier son L à un moment donén, c'est de faire des échanges bénéficiaires avec son environnement.
Ces échanges peuvent être énergétiques, informationnels ou monétaires.
On peut appeler liberté, ou autonomie absolue, d'un sujet, ce que devient son L si l'on suppose (note 92: supprime?) tous ses interfaces avec l'extérieur.
Dans le cas des sujets pensants, on peut dans une certaine mesure parler d'interface avec un environnement virutel. Le sujet n'est pas en effet totalement conscient de lui-même. Sans interfaces avec un organisme extérieur, il peut modifier son L en prenant plus ou moins possession de lui-même. Il peut l'accroître, par exemple, en faisant jouer son imagination, ou en ravivant -c'est à dire en augmentant la quantité d'information portée par- ses souvenirs.
Par ailleurs, et il faudrait montrer comment cela prend uns signification mathématique, il y a des contrôles réciproques avec d'autres sujets.
J'accrois mon L en prenant le contrôle d'un autre sujet, puisque en quelque sorte ses états viennent s'ajouter aux miens. Pour cet autre sujet, supposé totalement contrôlé, L devient nul puisqu'il ne peut plus shoisir entre ses différents états: c'est moi qui choisis.
Ici, la formule choisie pour L n'est pas satisafaisante. En effet, il faut que L de l'autre soit annulé, alors que, précisément, s'il est totalement asservi, son avenir est devenu totalement aléatoire puisque dépendant de mon bon plaisir.
Il va de soi que, dans la pratique, les contrôles sont toujours partiels, sauf les cas de pure matière (assimilation par digestion d'un objet alimentaires), ou léthaux: entuant l'autre, je ramène son L à zéro, bien sûr.
On aura ici les bases pour réfléchir aux distinctions entre valeur d'échange et valeur d'usage.
Convergence et antisystème (I)
L'histoire des systèmes se renouvelle à travers de très nombreux domaines, et présente des évolutions communes dont le chantre peut-être le plus inconditionnel mais le plus grandiose a été Teilhard de Chardin. Plus près de nous, un Prigogine continue d'en travailler le mouvement.
On montrera sans doute que la courbe de croissance est une fonction du genre de notre L. Une formulation de ce type montre bien que les systèmes devraient croitre en complexité. Que, par ailleurs, la possibilité d'accroître le nombre des états avec une faible énergie grâce aux facultés cognitives devrait être exploitée et conduire logiquement à la montée vers le plus grand cerveau.
Les systèmes informatiques sont une illustration assez frappante de ces évoluions. Point de convergence de très nombreuses techniques, l'ordinateur, c'est à dire l'automate calculateur, s'assimile puet à peu toutes les technologies: il remplace progressivement, par le biais de ses mémoires, tous les autres modes de stockage de l'information, y compris l'information visuelle (même si, sur ce point, la colonisation est moins radicale en raison de la masse des informations élémentaires). Il s'assimile tous les modules de transmission de l'information: les réseaux de télécomunication de demain seront entièrement digitaux.
Et non seulement sa transmission physique d'un point à un autre mais sa mise en forme, pour jouer un rôle important dans les systèmes d'enseignement (Encore que, sur ce point, les résultats ne soient pas à la hauteur des espérances !). Surtout, il prend progressivemnet le contrôle, par les automatismes industriels de plus en plus évolués, de la totalité du monde matériel, et sa maîtrise devient co-extensive à la nôtre. Y comoris, très largement, dans le domaine artistique. Il devient le coeur même de nos systèmes décisionnels. Etc.
Ce mouvement est provoqué à la fois par le dynamisme des systèmes informatiques et par les besoins des domaines colonisés. Détaillons en par exemple trois domaines: la mesure, la saisie des données, et les télécommunications. Un prochain article d'Informatique et Gestion traitera de la convergence avec l'informatique industrielle.
La mesure
On mesurait peu, autrefois. A quoi bon, d'ailleurs, si les problèmes se résolvent à la manière des savants de Jules Verne (De la Terre à la Lune, page 113 dans l'édition Hetzel):
"Maintenant, mes amis, quelle quantité de poudre proposez-vous?"
Les trois membres du Gun-Club s'entre-regardèrent un instant.
"Deux cent mille lvres" dit enfin Morgan.
- Cinq cent mille, répliqua le major.
- Huit cent mille livres !" s'écria J.T. Maston...
A quelques exceptions près, essentiellement dues aux astronomes, une faible précision suffisait donc. La situation a changé, et l'on ne cesse de rechercher de nouvelles décimales sur les constantes fondamentales (La Recherche...). De plus, et nous retrouverons le fait sous de nombreux angles, il est devenu indispensable d'assurer la cohérence des mesures, grâce par exemple aux systèmes d'unités.
La précision s'accroît, mais aussi la variété des mesures prises. Le catalogue d'une exposition comme Mesucora a de quoi laisser rêveur. Des jauges de contrainte aux anémomètres, en passnat par les compteurs Geiger, les types de capteurs se comptent par centaines, qu'il faut multiplier par les différentes plages couvertes, de l'infrarouge aux ultraviolets, du micromètre au télémètre... j'en passe et des meilleurs.
Et le nombre des mesureS prises augmente lui aussi de façon vertigineuse. Qu'on songe à la multitude de capteurs placés dans la nacelle du Concorde pour ses essais. A la production de centres comme les souffleries de Modane, qui ne sont pratiquement que de grandes usines à mesurer. Les performances des systèmes d'acquisition de données sont d'ailleurs éloquentes: 100 000
mesures à la seconde pour le système étudié par Sup'Aéro à Toulouse.
Avec la croissance, le nom lui-même a changé: on ne mesure plus, on acquiert des données (data logging). L'informatique est passée par là. Car, bien entendu, pas question d'exploiter manuellemenet de pareilles masses de chiffres. Seul l'ordinateur est à la masure (une de plus) du problème.
Pour en venir là, il a fallu automatiser largement la mesure, créer des systèmes "multiplexeurs" tâtant successivement, à une cadence très rapide, les différents points examinés. Il a fallu aussi la "numériser", c'est à dire transformer en information binaire l'information autrefois fourne sous forme analogique: cadran ou tension continue. Les chiffres avancés montrent que le calculateur est le moyen le plus aisé d'automatiser ces fonctions (une fois exécutée la conversion analogique/digital). Et il est présent dans un nombre croissant de systèmes de mesure, et même jusqu'aux plus classiques, comme ces puissantes pinces à étirer le métal qui servent à en mesurer la ténacité, c'est à dire la résistance à la rupture par traction.
De petits calculateurs comme les PDP de Digital Equipment ou le 9100 de Hewlett Packard sont appropriés aux petits systèmes. Et rien de plus symptomatique de cette évolution que la présence sur le stand de cette dernière firme, à Mesucora, d'un petit clavier de commande et de calcul associé aux instruments électroNiques de rigueur: oscilloscope et voltmètre numérisé.
Automatisée, la mesure peut devenir adaptative. L'antenne de radar adapte ses caractéristiques (projet Dassault pour 1980) et son orientation (antennes de poursuite) en fonction des résultats reçus. On pourrait facilement aussi rechercher la mesure à plusieurs niveaux, en passant au niveau de précision supérieur par adaptation du dispositif une fois acquis un certain niveau, comme un astronome pointe d'abord son puissant télescope au moyen d'une lunette plus modeste.
On va plus loin encore. Mesurer, c'est fournir un chiffre, certes. Mais on peut aussi rechercher des formes, des signaux caractéristiquEs dans un bruit plus ou moins fort. En chromatographie en phase gazeuse, par exemple (c'est à dire un système d'analyse des gaz par mesure des différences de vitesse de déplacemnet de ses constituants dans un tube long et étroit en fonction de leur viscosité), on détectera les "pices", c'est à dire que l'on analysera, automatiquement, la courbe brute fournie par l'appareil, afin d'obtenir des valeurs numériques pour la concentration de chacun des composants. Cette mesure fait donc appel -sous une forme assez élémentaire- aux techniques de la reconnaissance des formes, pour traduire dans un langage formalisé et directement utilisable soit par le chercheur, soit par un calculateur, soit par des appareils automatiques, le résultat d'une opération complexe.
Autre exemple, l'extracteur radar est un sytsème informatique analysant les échos fournis par un radar et les traduisant en termes de cibles, passant si l'on peut dire du travail rétinien du radar au travail cérébral de la définition et de la dénomination d'objets.
Ce traitement effectué sur la mesure brute comporte, au passage, toutes sortes d'opérations de contrôle et de corrélation des différents résultats obtenus. Le résultat de la mesure est donc plus fiable, outre qu'il est plus facile d'emploi.
D'importants travaux sont menés au MIT. L'un des systèmes étudiés comporte une main mécanique commandée par un ordinateur en fonction de ce qu'il voit par l'intermédiaire d'une caméra de télévision. L'appareil parvient à chercher dans une boite de volumes en boais l'analogue d'un modèle présenté devant la caméra. Il peut aussi, avec quelques difficultés, à partir de la même boite de cubes, faire une construction identique à un montage qui lui est montré. Les performances ne sont pas très brillantes, le prix n'est certes pas compétitif. Mais le fait est important.
Précise, globalisante, fiable, identificatrice d'objets, la mesure doit aussi devenir conversationnelle. Son audo-adaptativité lui a permis de cerner un certain type d'objets. Dans beaucoup de cas, cependant, l'homme reste le seul à pouvoir appréhender suffisamment les objectifs fixés et leur contexte; et c'est lui qui guidera le capteur vers le résultat précis recherche. C'est une des raisons qui justifie la présence de l'homme dans l'espace, et non seulement d'automates.
Mais cette notion de conversationnel nous conduit à un cas particulier d'introduction d'information dans le système: la saisie des données.
Notons cependant un point important: à force de mesurer l'univers et d'en faire la conquête, l'homme va trouver à mesurer essentiellement l'homme. Sans parler du domaine médical, les capteurs travaillent de manière croissante sur des éléments créés par l'homme. Jusqu'aux plus classiques d'entre eux: comme chacun sait, il n'y a plus de saisons depuis la bombe atomique, et les
baromètres nous renvoient l'image de nos explosions atomiques... pour ne pas parler des sismographes, créés à l'origine pour connaître les forces secrètes de la terre et devenus détecteurs d'expériences nucléaires.
(note 92: la nature se défend tout de même enocre, éruptions et surtout épidémies, Sida).
(note 2014: l'anthropocène...)
L'évolution de la mesure, quantitativement et qualitativemnet, l'a donc conduit à devenir essentiellement le versant "capteur" (ou si l'on préfère, le système sensoriel), des systèmes informatiques. Sa croissance numérique à elle seule exige le calculateur (il faut plusieurs Univac 1108, en permanence, pour un premier dépouillement, un simple tri, des flots de mesure reçus des satellites). Sa complexité exige l'appel à des disposifits cybernétiques de plus en plus élaborés que seul le calculateur est à même de fournir économiquement et avec souplesse.