Alcyone, by Hugo Verlinde. He was early captivated by the beauty of transcendent functions.

Digital Art and Mathematics. A short review.

That's quite a vast topic. We propose here some short notes, using diccan and my own experiences with Roxame.
Pierre Berger. Version published on Jan. 24, 2018. To be revised.

1. Kinds of mathematics used by digital artists
2. Digial artists origins and courses

1. Kinds of mathematics used

We sort them by their place in the art creation process steps

1.0 Global creation process control

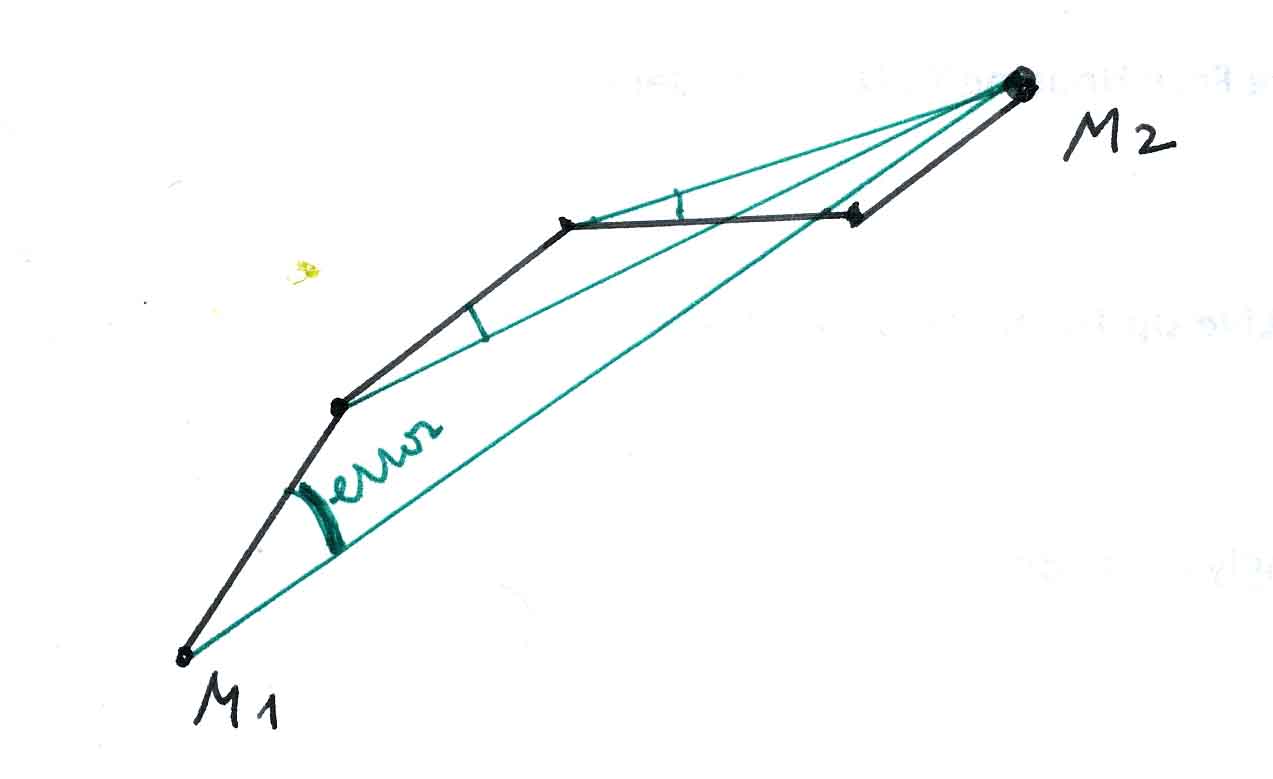
A random function used by Roxame to generate "live" lines drawing. The classical "LineTo" function is broken into several segments, each one oriented towards the target point, but with an error on the angle. Chossing the error rate, the "ubris" can be trimmed from "cold" to "frenzied".

- Linguistics of macro-instructions (e.g. Roxame's dictionary).
- Logic, recursion, as far as they are mathematic, see below. And generally, mathematical laws emb embedded in digital hardware and software.
- Random numbers (an important component in generative art [Berger-Lioret], chaos, complexity, emergence.

1.1. Abstract creation and expression

- Harmony in proportions (golden section) and symmetry [Funck-Hellet].
- Algorithms for form generation (e.g. Bresenham for straight lines), see notably [Foley]. trigonometry, perhaps manifolds, topology (at least implicitly). The most sophisticated generative algorithms are used by the animation industru (Mac Guff, Pixar).
- Fractals. Many artists, though limited results.
- Matrices [Le Boucher, robotics].
- Mathematics embedded in graphic softwre, notable 3D modeling.
- Shapes/forms grammars, L-grammaires et L-systems (Miguel Chevalier, for videos of vegetals), Jean-Pierre Balpe for writing... But musical harmony rules, and contrepoint, may be considered as such, including derialist music.

High level mathematics are basic to get fun! (Here an image from Osuka's course on 3D meshes).

- Data visualization, using algorithms to get meaning out of data
- Icons sets, which can be used mathematically
- Euclidean space modeling (perpective)
- Materials modeling with their deformations (notably liquids and spreads)
- Body models (Poser software, Michel Bret)
- Materials resistance in architecture (but this used in not explicited in literature on the subject).
- Biology, life properties, darwinism ( [Whitelaw], Sommerer & Mignonneau
- Data analysis , dataviz, datascape. Mainly used for practical uses (management, communication), but possibly also with properly artistic views. For instance the worldwide emotions statitics in the transmedia work of Maurice Benayoun).
- Baker's transform (a curioisty with little use)
- Symmetry (rare, some uses in Roxame)
neural networks (Michel Bret, some recent Siggraph references)
- Choreographic proposals (Laban language)

1.2. Signal processing (images, sound)

Michel Bret uses neural networks and their deep mathematical funcgions to control the movements of his dancers.

- Filtering, convolution/deconvolution (Roxame)
- Analog/Digital conversion, coding.
- Acqusisition of data for modeling (scanning, Gehry.)
- Compression/decompression (generally not shown, but used artistically. glitch by Jacques Perconte).
- Pattern recognition. OpenCV (Roxame, Rafael Lozano-Hemmer).
- Perception in general
- Body perception (dance, mocap) and interaction in performance (Gourfink.)
- Morphogeometry (convolution/deconvolution, notamment pour obtenir des contours ou pour le sharpening).

An example of texture by David Ebert

1.3. Expression, rendering

Mathematical models of light and color (RGB, HSV)
Textures [Ebert], lighting processes, tiling.
Sound generators , synthesizers, amplification
Peripherals driving (printers, screens..)

1.3 Evaluation

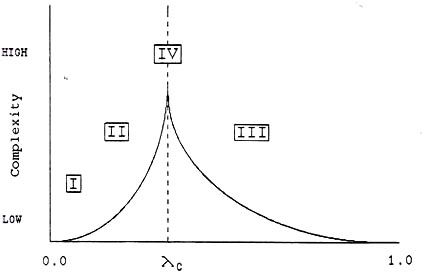
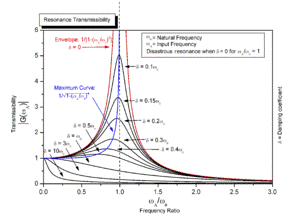
A mathematical evaluation of meaning and beauty seems quite blasphemous. But some results are provided by complexity measurement, artificial life experiments or analogy with resonance.

We mean here aestheric evaluation, with all the disputable aspects of such a modeling.

- Proportions (golden section)
- Measurement of meaning ([Moles], [Osgood], in Roxame). Mainly shannonian. A balance between order and chaos. See our communication at Laval Virtual.
- Statistical and empiric evaluation by the collectors, the public and the market. Customer profiling (Google...).

An example of interaction by Rafael Lozano-Hemmer.

1.4 Behavior and Interaction

- Behavior models, gameplay, storytelling
learning
- Formal lingustics, Markov chains.
- Smart buildings
- Neural networks, retropropagation

2. Artists origins, profiles and courses

Clarissa, by Harold Cohen . He was a successful traditional painter when he fell in love with computing. Then developed original solutions for drawing and coloring.

As far as we know, no professional mathematician ever became a digital artist, but on occasion or for fun. The main courses we observe are:

- starting from algorithmics, before computer advent: Joseph Schillinger, Manfred Mohr, Vera Molnar,
- starting from a mathematical inspiration: Hugo Verlinde, Anne-Sarah Le Meur, Evelyne Lutton, Alain Le Boucher
- starting grom a computer inspiration: Harold Cohen, Antoine Schmitt, Christian Lavigne, Pierre Berger
- using the computer as a mere tool : l'informatique graphique, Siggraph
- cooperation with computer professionals : Wenger/Chevalier, Pascal Bauer